Електронна оптика електростатичних полів». Розподіл потенціалу в аксиально-симетричному електричному полі, страница 3

1.3  Методи, що використовуються для розв’язання задачі.

1.3.1  Метод кінцевих різниць для розрахунку поля електростатичних лінз.

Аналітичний розрахунок електричного поля (розв’язок рівняння Лапласа) може бути виконаний тільки у найпростіших випадках. Але навіть тоді, коли вдається отримати аналітичний розв’язок, кінцеві вирази часто опиняються громіздкими и не досить зручними для практичного використання. Тому при розв’язанні електронно-оптичних завдань широко використовуються наближені методи розрахунку і експериментального дослідження електричних полів.

В основі методу кінцевих різниць лежить заміна похідних в вихідному рівнянні невеликими різницями. Припустимо, що необхідно знайти розподіл потенціалу у просторі між двома непаралельними пластинами відхиляючої системи електронно-променевої трубки. (мал.1.2)

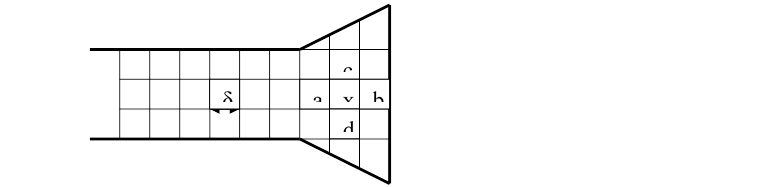
Мал.1.2 Приклад знаходження потенціалу.

Розіб’ємо увесь простір між пластинами на клітинки з рівними сторонами δ. Неважко показати, що величина потенціалу U_x в точці x, рівновіддаленої від точок a, b, c, d з відомими величинами потенціалів U_a, U_b, U_c, U_d  може бути визначена як:

                                                  (1.13)

Зіставимо різниці:

При достатньо малих значеннях δ можна покласти, що ці різниці приблизно рівні

Використовуючи повторно таку ж операцію, отримаємо

            -                                                                                    (1.14)

-

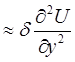
Складаючи рівняння (1.14), отримаємо в правій частині рівняння Лапласа:

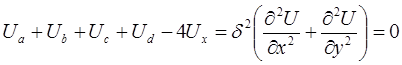                           (1.15)

З (1.15) безпосередньо випливає (1.13). Розв’язок кінечно-різничного рівняння може бути виконано методом послідовних наближень (метод ітерацій).

Задаючи граничні значення потенціалу на електродах, можна орієнтовно нанести величини  U a₁, a₂, …, b₁, b₂, …, c₁, c₂, …, d₁, d₂, …  і підрахувати згідно з (1.13) значення потенціалу в точках x₁, x_{2, … .} Після цього прийняв знайдені величини U_x за вихідні, потрібно перерахувати значення потенціалів в точках a, b, c, d, знову уточнити величину U_x і т.д. Повторюючи такий прийом декілька разів можна поступово наблизитись до точних значень потенціалу усього простору. Часто 4-5-е наближення мало відрізняється від попереднього, і подальшого уточнення не потребується.

Вказаний метод може бути використаний для розрахунку не тільки плоских, а й осесиметричних полів. В цьому випадку значення потенціалу в точках площини, що проходить скрізь вісь системи (меридіональної площини), визначається виразом:

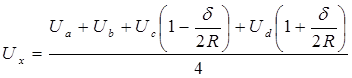                                    (1.16)

де R–відстань точки х від осі системи.

Визначив шляхом послідовних наближень значення потенціалу в усіх точках досліджуваного поля і з’єднав точки з однаковими потенціалами неперервними кривими, отримаємо картину еквіпотенціальних ліній, що достатньо повно характеризують електронно-оптичну систему. 

1.3.2  Метод лінійних відрізків осьового потенціалу при розрахунку траєкторій електронів в електростатичному полі лінзи.

Рівняння руху електронів в електричних полях лише в рідких випадках можуть бути розв’язані аналітично. Тому практично для знаходження траєкторій електронів, що рухаються в електричних полях, потрібно або використовувати наближені методи розв’язку основних рівнянь, або будувати траєкторії графо-аналітично.

У тих випадках, коли осьовий розподіл потенціалу, знайдений експериментально або визначений наближено, не піддається апроксимації аналітичною функцією, може бути використаний метод наближеного розв’язку основного рівняння, що отримав назву метода многокутників або методу лінійних відрізків осьового потенціалу. При використанні цього методу область осесиметричного електричного поля, в якій необхідно знайти траєкторію параксіального електрону, розбивається на низку ділянок, усередині кожної з яких осьовий розподіл потенціалу представляється лінійною функцією z, тобто напруженість поля є постійною усередині кожної ділянки і змінюється стрибком при переході до іншої ділянки. Іншими словами, плавна крива розподілу осьового потенціалу замінюється ломаною, що складається з відрізків прямих. (мал.1.3)