Знаючи значення складових напруженості електричного поля можна перейти до аналізу процесів руху параксиальних електронів в аксиально-симетричному електричному полі.
Зазначимо також, що у вигляду осьової симетрії поля, складова його
напруженості в напрямі азимута ![]() дорівнює нулю і
електрон, що ввійшов в поле в якійсь площині (в меридіональній площині), буде продовжувати рухатися в цій же
площині, тобто траєкторія його буде плоскою кривою.
дорівнює нулю і
електрон, що ввійшов в поле в якійсь площині (в меридіональній площині), буде продовжувати рухатися в цій же
площині, тобто траєкторія його буде плоскою кривою.
Для аксиально-симетричного електричного поля рівняння руху електрона мають вигляд:
![]()
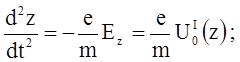 (1.8)
(1.8)
![]() (1.9)
(1.9)
Вирішуючи ці рівняння і виключаючи з них час отримуємо вираження, що описує траєкторію рухомої частки:
![]() (1.10)
(1.10)
Якщо провести диференціювання в лівій частині рівняння (1.10), то воно приводиться до більш зручному для аналізу вигляду:
![]() (1.11)
(1.11)
Рівняння (1.10) і (1.11) є дві форми одного і того ж співвідношення, яке являє собою рішення рівнянь руху зарядженої частки в аксиально-симетричному електричному полі і яке зв'язує координати її руху r і z. Отже, це є виражене в диференціальній формі рівняння траєкторії будь-якого параксиального електрона в аксиально-симетричному електричному полі. Щоб отримати рівняння траєкторії конкретного електрона в явному вигляді, необхідно проінтегрувати диференціальне рівняння траєкторії (1.11) при відповідних даному електрону початкових умовах. Цими умовами будуть відстань електрона від осі, кут нахилу траєкторії до осі, а також величина різниці потенціалів, пройдена електроном в момент входу його в поле.
Точне аналітичне рішення диференціального рівняння траєкторії (1.11) в більшості практично цікавих випадків являє собою вельми складну задачу. Однак навіть в своєму загальному вигляді воно дозволяє зробити цілий ряд важливих практичних висновків:
1) У рівняння входить тільки розподіл потенціалу по осі симетрії поля U(z). Тому траєкторія параксиального електрона визначається розподілом потенціалу на осі поля і граничними умовами, відповідними конкретному електрону.
2) У рівняння не входять ні заряд, ні маса рухомої в полі зарядженої частки. Це означає, що не тільки електрони, але і будь-які заряджені частки, в тому числі і набагато більш важкі негативні іони, будуть при співпадаючих початкових умовах рухатися по одних і тих же траєкторіях.
3) Рівняння (1.11) лінійне і однорідне відносно U(z). Це означає, що потенціал і його похідні входять в рівняння в першій степені і, крім того, права частина рівняння дорівнює нулю. Звідси відразу слідує, що якщо потенціали всіх електродів, що створюють поле, змінити на одне і теж число, то траєкторії електронів залишаються незмінними.
4) Рівняння лінійно і однорідно також і відносно r(z). Тому, якщо модель є збільшеною копією електродів електронно-оптичної системи, то траєкторії електронів в ній залишаються геометрично подібними траєкторіям в реальній системі.
5) Будь-яке аксиально-симетричне поле є електронною лінзою і може створювати зображення за допомогою параксиальних електронів.
Сила, з якою аксиально-симетричне електростатичне поле діє на рухомий електрон в радіальному напрямі, дорівнює:
![]() (1.12)
(1.12)
Отже, якщо U"(z)>0, що відповідає наростанню напруженості поля вздовж осі z, радіальна сила направлена протилежно напряму вектора r, тобто до осі z. При цьому, траєкторія електрона буде згинатися до осі симетрії поля, яке, діючи на рухомий пучок параксиальних електронів, буде прагнути зібрати його до осі симетрії.
У випадку ж, якщо U"(z)<0, радіальна сила направлена від осі z і пучок буде розсіюватися.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.