ЗАДАНИЕ ДЛЯ КУРСОВОЙ РАБОТЫ
1. Получить передаточные функции звеньев и определить их тип.
2. Составить структурную схему САР.
3. Рассчитать и построить амплитудно-фазовые характеристики, асимптотические ЛАЧХ и ЛФЧХ, переходные и весовые характеристики соединения второго и пятого звеньев. Номер динамического звена совпадает с номером уравнений в исходной системе уравнений.
4. По структурной схеме САР получить передаточную функцию разомкнутой системы по цепи главной обратной связи системы, а также передаточные функции замкнутой системы для регулируемой величины и ошибки по задающему воздействию.
5. Построить логарифмические частотные характеристики разомкнутой системы.
6. Проверить замкнутую систему на устойчивость. Определить запасы устойчивости по модулю и фазе.
7.
Рассчитать
установившуюся ошибку слежения за задающим воздействием ![]() ,
где скорость принять равной
,
где скорость принять равной ![]() с-1
для всех вариантов задания.
с-1
для всех вариантов задания.
ЗАДАНИЕ
Задана исходная система уравнений динамики системы автоматического регулирования (САР)
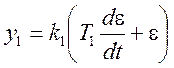 ; (1)
; (1)
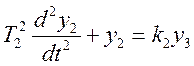 ; (2)
; (2)
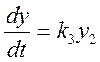 ; (3)
; (3)
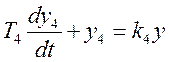 ; (4)
; (4)
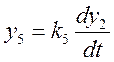 ; (5)
; (5)
![]() ; (6)
; (6)
![]() ; (7)
; (7)
где ![]() - регулируемая величина;
- регулируемая величина; ![]() - задающее воздействие;
- задающее воздействие;
![]() -
ошибка регулирования;
-
ошибка регулирования; ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() - промежуточные координаты;
- промежуточные координаты; ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() - передаточные коэффициенты звеньев;
- передаточные коэффициенты звеньев; ![]() ,
, ![]() ,
, ![]() - постоянные времени.
- постоянные времени.
Таблица 1:
|
Пара- метр |
№ варианта |
|
1.10 |
|
|
|
163 |
|
|
9,2 |
|
|
0,2 |
|
|
2 |
|
|
0,073 |
|
|
70 |
|
|
58 |
|
|
4 |
Приведение постоянных времени
звеньев к системе СИ
![]()
![]()
![]()
1 ПРЕДСТАВЛЕНИЕ ИСХОДНОЙ СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ИЗОБРАЖЕНИЯХ ПО ЛАПЛАСУ ПРИ НУЛЕВЫХ НАЧАЛЬНЫХ УСЛОВИЯХ. ПОЛУЧЕНИЕ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ ЗВЕНЬЕВ И ОПРЕДЕЛЕНИЕ ИХ ТИПА
Для исходной системы дифференциальных уравнений проделаем прямое преобразование Лапласа при нулевых начальных условиях
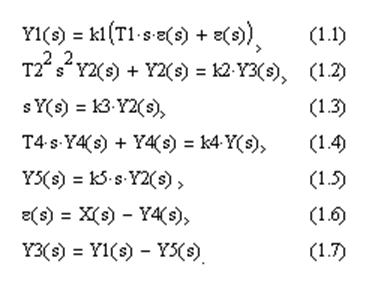
Уравнения динамики в изображениях для звеньев
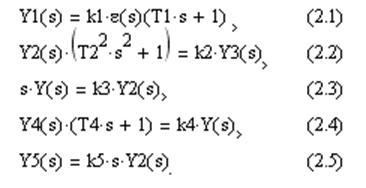
Уравнения динамики в изображениях для сумматоров
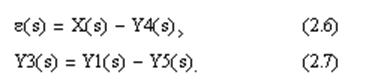
По полученной системе уравнений найдём передаточные функции звеньев и определим их тип

2 СОСТАВЛЕНИЕ СТРУКТУРНОЙ СХЕМЫ САР

Рисунок 1. Структурная схема САР с двумя отрицательными обратными связями
3 РАСЧЕТ И ПОСТРОЕНИЕ АМПЛИТУДНО-ФАЗОВЫХ ХАРАКТЕРИСТИК, АСИМПТОТИЧЕСКИХ Л.А.Ч.Х. И Л.Ф.Ч.Х., ПЕРЕХОДНЫХ И ВЕСОВЫХ ХАРАКТЕРИСТИК ДЛЯ СОЕДИНЕНИЯ ВТОРОГО И ПЯТОГО ЗВЕНЬЕВ
Номер динамического звена совпадает с номером уравнений в исходной системе уравнений.
Передаточная функция соединения второго и пятого звеньев:
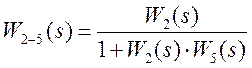 .
(3.1)
.
(3.1)
Подставляем значения передаточных функций звеньев данного соединения:
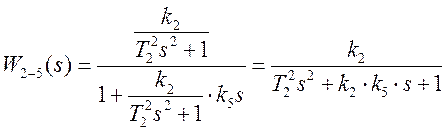 . (3.2)
. (3.2)
Преобразуем коэффициенты слагаемых знаменателя:
![]() ,
(3.3)
,
(3.3)
![]() ,
,
![]()
Таким образом:
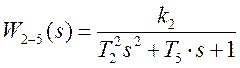 - инерционное звено 2-го
порядка. (3.4)
- инерционное звено 2-го
порядка. (3.4)![]()
3.1 Расчёт и построение амплитудно-фазовой характеристики соединения 2-го и 5-го звеньев
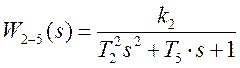 .
.
Заменяем s на jω:
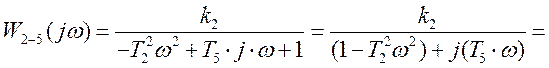
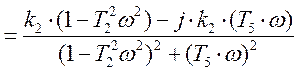 .
(3.5)
.
(3.5)
W(jω)=U + jV- амплитудно-фазовая характеристика, где:
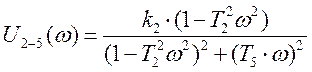 , - вещественная часть (3.6)
, - вещественная часть (3.6)
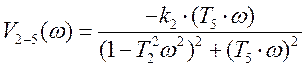 . – мнимая часть
(3.7)
. – мнимая часть
(3.7)
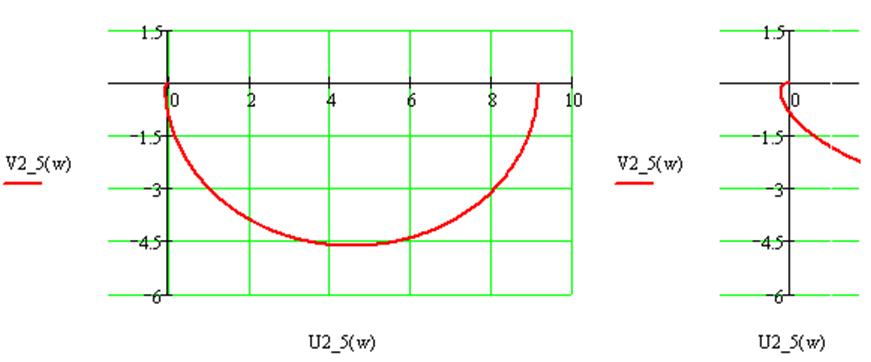
Рисунок 2. АФХ соединения 2-го и 5-го звеньев
3.2 Расчёт асимптотической Л.А.Ч.Х. соединения 2-го и 5-го звеньев
![]()
![]()
![]()
Т.к. ![]() ,
то можно разложить знаменатель на произведение сомножителей:
,
то можно разложить знаменатель на произведение сомножителей:
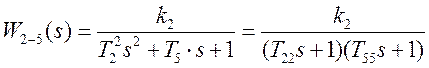 (3.8)
(3.8)
- получили последовательное соединение двух апериодических звеньев 1-го порядка и одного усилительного
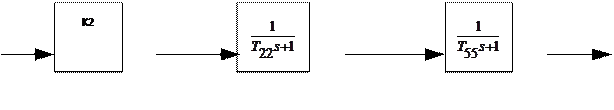 |
![]() , (3.9)
, (3.9)
![]() (3.10)
(3.10)
Частоты сопряжения звеньев
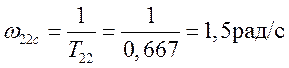 ,
(3.11)
,
(3.11)
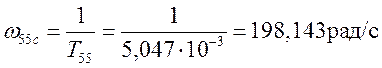 .
(3.12)
.
(3.12)
3.3 Расчёт Л.Ф.Ч.Х. соединения 2-го и 5-го звеньев
а) Передаточная функция апериодического звена 1-го порядка в общем случае:
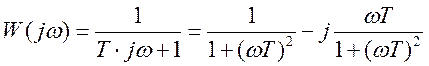 .
(3.13)
.
(3.13)
Действительная часть:
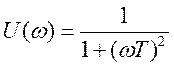 .
(3.14)
.
(3.14)
Мнимая часть:
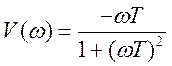 .
(3.15)
.
(3.15)
Фазово-частотная характеристика этого звена:
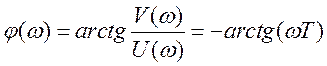 .
(3.16)
.
(3.16)
б) Передаточная функция идеального усилительного звена в общем случае:
![]() .
(3.17)
.
(3.17)
Действительная часть:
![]() .
(3.18)
.
(3.18)
Мнимая часть:
![]() .
(3.19)
.
(3.19)
Фазово-частотная характеристика этого звена:
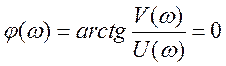 .
(3.20)
.
(3.20)
Т.к. ![]() можно представить в виде
последовательно соединенных звеньев, то ее Л.А.Ч.Х. и Л.Ф.Ч.Х. будут
складываться из суммы Л.А.Ч.Х. и Л.Ф.Ч.Х. соответственно этих звеньев.
можно представить в виде
последовательно соединенных звеньев, то ее Л.А.Ч.Х. и Л.Ф.Ч.Х. будут
складываться из суммы Л.А.Ч.Х. и Л.Ф.Ч.Х. соответственно этих звеньев.
Построим асимптотические Л.А.Ч.Х. и Л.Ф.Ч.Х. на основании рассчитанных выше данных и характеристик типовых динамических звеньев.
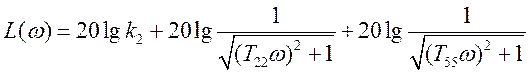
![]()
3.4 Построение асимптотических Л.А.Ч.Х и Л.Ф.Ч.Х
Л.А.Ч.Х. соединения 2-го и 5-го звеньев:
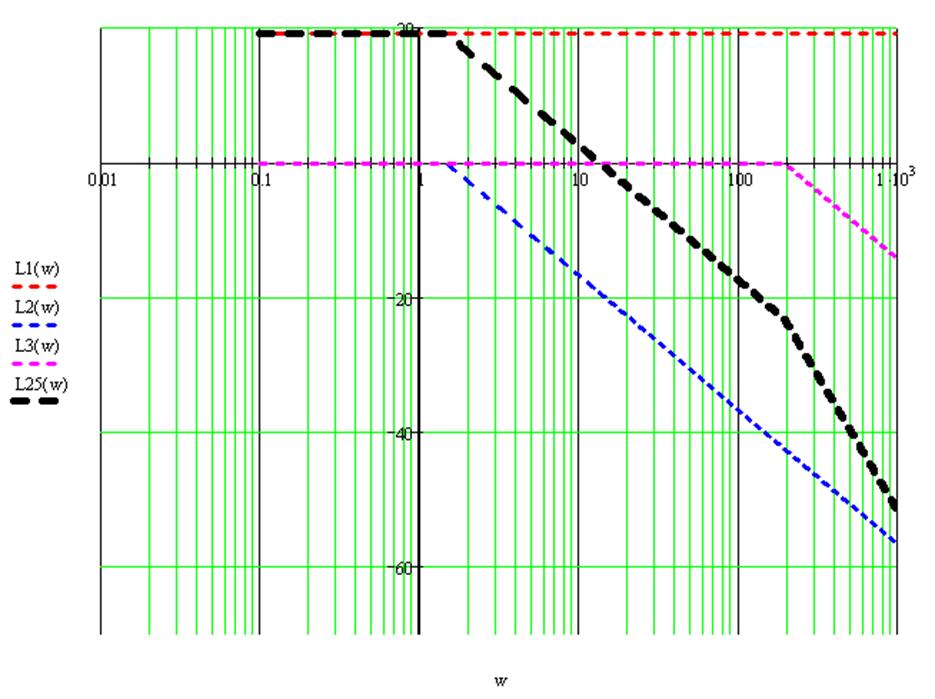
Л.Ф.Ч.Х. соединения 2-го и 5-го звеньев: 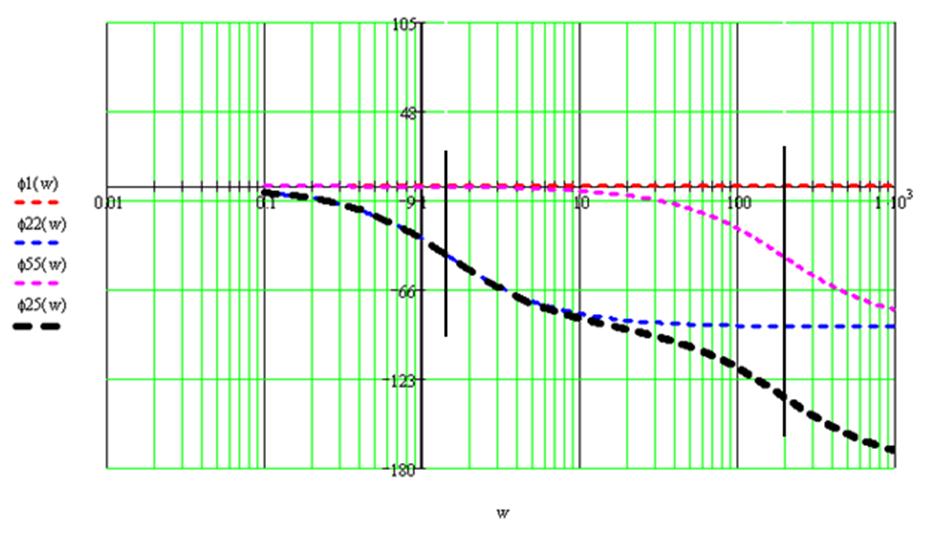
3.5 Переходная характеристика соединения 2-го и 5-го звеньев
Используя таблицу преобразования найдём переходную функцию
звена ![]() :
:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.