САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
БАЛАКОВСКИЙ ИНСТИТУТ ТЕХНИКИ, ТЕХНОЛОГИИ И УПРАВЛЕНИЯ
ФАКУЛЬТЕТ ИНЖЕНЕРНО-СТРОИТЕЛЬНЫЙ
КАФЕДРА «УПРАВЛЕНИЕ И ИНФОРМАТИКА В ТЕХНИЧЕСКИХ СИСТЕМАХ»
ЛАБОРАТОРНАЯ РАБОТА №5
по дисциплине «ТАУ»
ИССЛЕДОВАНИЕ ЛИНЕЙНЫХ СИСТЕМ
АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
С ПОМОЩЬЮ D-РАЗБИЕНИЯ
Выполнил: ст.гр. УИТ-31
Душина Д.В.
Принял:
Шумарова О.С.
2011
Вариант №8.
Цель работы:
1. Исследовать влияние параметров системы (регулятора) на устойчивость и качество регулирования.
2. Освоение методики построения кривой D-разбиения в плоскости 2-х параметров.
Задание.
Представлена структурная схема исследуемой системы:
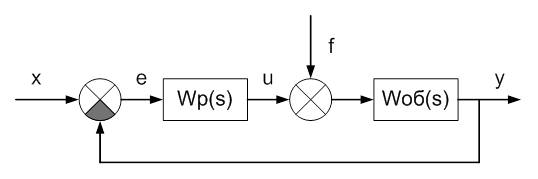
Рис. 1 – Структурная схема системы регулирования
Звенья системы:
![]()
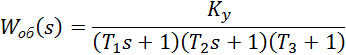
Параметры объекта:
![]()
![]()
![]()
![]()
Определить критические значения для
коэффициентов ![]() и
и ![]()
Методом D-разбиений построить границу области устойчивости в плоскости
параметров ![]() и
и ![]()
Исследовать качество процессов при
различных значений ![]() и
и ![]() методом сканирования.
методом сканирования.
Для каждой пары значений построить переходную кривую, а также определить временные характеристики.
Ход выполнения.
Определим общую передаточную функцию и подставим известные числовые значения.
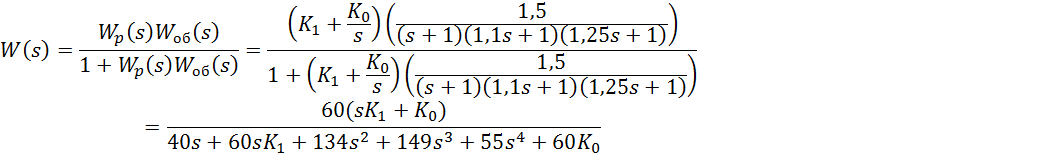
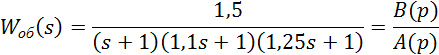
Характеристическое уравнение
замкнутой системы: ![]() , где
, где ![]()
![]()
![]()
Подставим ![]()
![]() - уравнение границы D-разбиения в плоскости
- уравнение границы D-разбиения в плоскости ![]() ,
, ![]()
Выделим в этом уравнении вещественную и мнимую части и приравняем по отдельности к 0:
![]() ,
, ![]() , где
, где 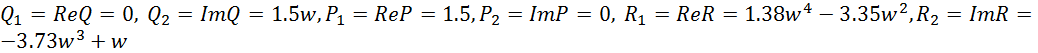
Решим уравнения методом
определителей: ![]()
![]()
![]()
Рассчитаем критические значения ![]()
![]()
![]()
Построим границу области устойчивости
в плоскости параметров ![]()
![]() методом D-разбиения:
методом D-разбиения:
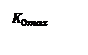
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
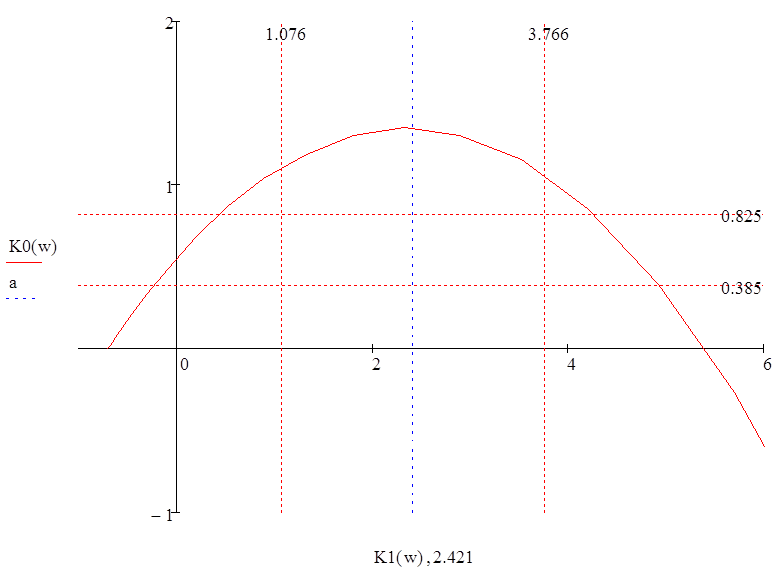
Рис. 2 – Разбиение области устойчивости при методе сканирования
На графике отмечены 10 точек внутри области, которые будут исследоваться далее.Каждой точке соответствует своя пара коэффициентов, определяющих настройки системы. Для каждой точки проведем исследования на устойчивость, построим переходную кривую, а также найдем временные характеристики.
Ниже представлены графики переходных процессов для каждой пары точек:
1ая точка
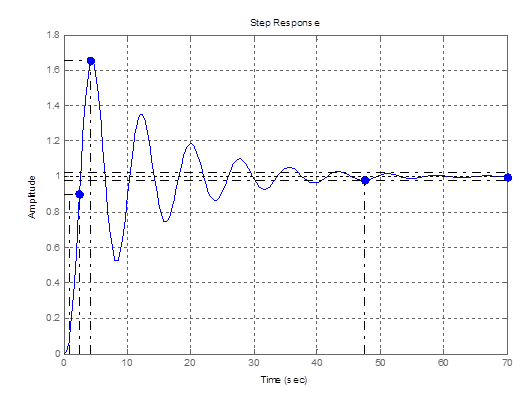
Рис. 3 – График переходной функции для 1ой точки
2ая точка
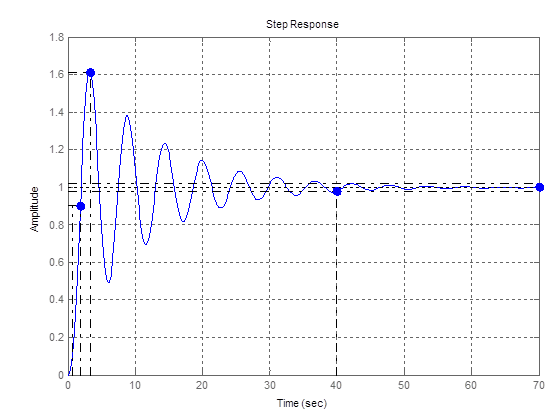
Рис. 4 – График переходной функции для 2ой точки
3ья точка
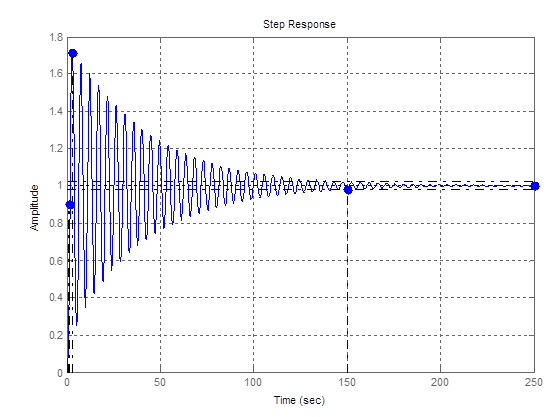
Рис. 5 – График переходной функции для 3ей точки
4ая точка
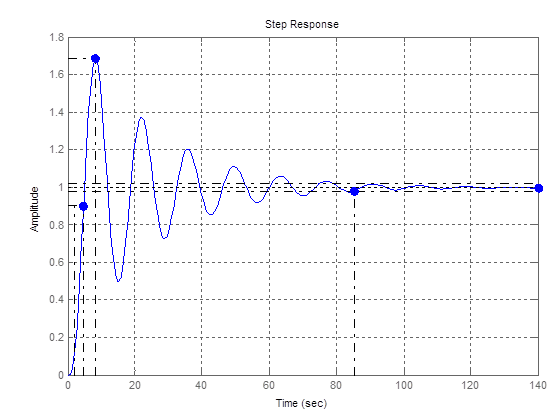
Рис. 6 – График переходной функции для 4ой точки
5ая точка
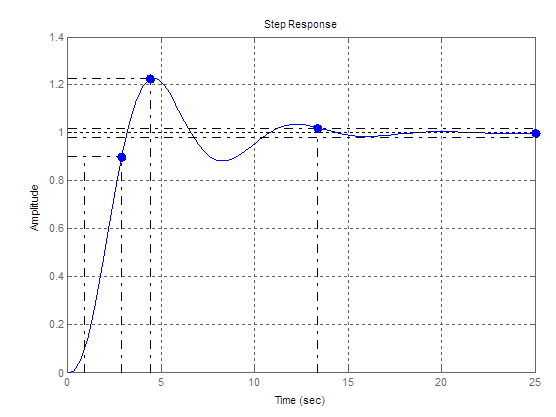
Рис. 7 – График переходной функции для 5ой точки
6ая точка

Рис. 8 – График переходной функции для 6ой точки
7ая точка
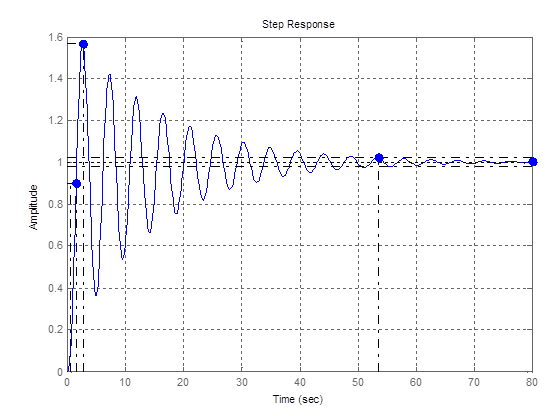
Рис. 9 – График переходной функции для 7ой точки
8ая точка
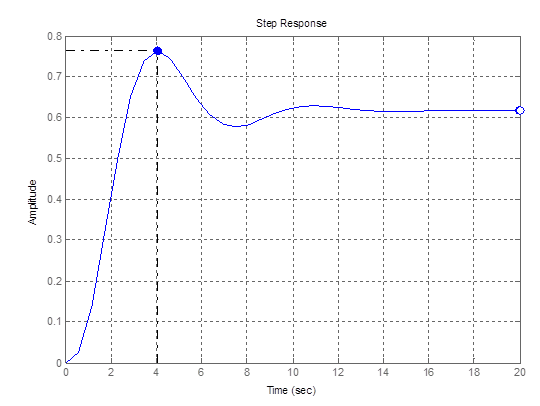
Рис. 10 – График переходной функции для 8ой точки
9ая точка
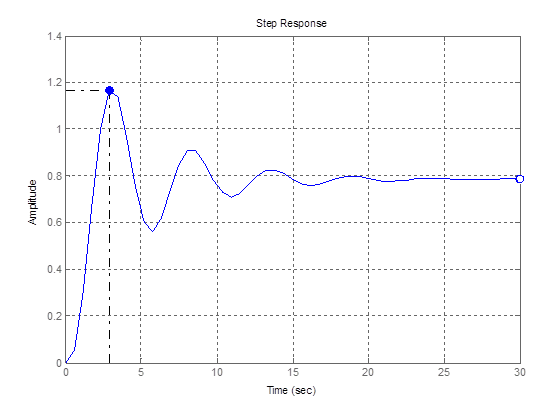
Рис. 11 – График переходной функции для 9ой точки
10ая точка
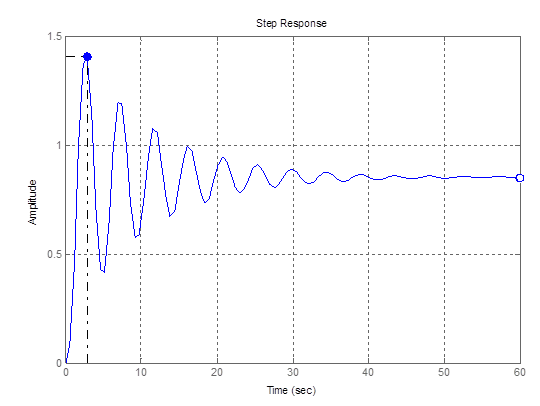
Рис. 12 – График переходной функции для 10ой точки
Результаты исследования представлены в таблице 1:
|
№ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
0,825 |
0,825 |
0,825 |
0,385 |
0,385 |
0,385 |
0,385 |
0 |
0 |
0 |
|
|
1,076 |
2,421 |
3,766 |
0 |
1,076 |
2,421 |
3,766 |
1,076 |
2,421 |
3,766 |
|
|
68 |
62 |
72 |
70 |
24 |
39 |
57 |
24 |
48 |
75 |
|
|
47 |
40 |
150 |
84 |
13 |
23 |
53 |
20 |
30 |
60 |
|
|
0,28 |
0,24 |
0,07 |
0,29 |
0,18 |
0,25 |
0,18 |
0,19 |
0,31 |
0,21 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0,38 |
0,21 |
0,2 |
Табл. 1 - Результаты исследования
Вывод: в работе была исследована система с двумя переменными коэффициентами, была построена граница D-разбиения и методом сканирования выбраны и проверены 10 точек, определяющих значения коэффициентов для системы. В конечном счете, подставляя только пять последних пар коэффициентов в передаточную функцию мы получали стабильную систему, эти пять точек находятся ближе всего к изгибу границы D-разбиений.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.