Исследование нелинейных САУ с помощью методов фазовых траекторий и припасовывания

МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ РФ

САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

БАЛАКОВСКИЙ ИНСТИТУТ ТЕХНИКИ, ТЕХНОЛОГИИ И УПРАВЛЕНИЯ

кафедра: УИТ

Практическая работа №1

ИССЛЕДОВАНИЕ НЕЛИНЕЙНЫХ САУ С ПОМОЩЬЮ

МЕТОДОВ ФАЗОВЫХ ТРАЕКТОРИЙ И ПРИПАСОВЫВАНИЯ

Вариант №6

Выполнил:

Ст.гр. УИТ-41

Горулев Р. А.

Принял:

Скоробогатова Т.Н.

2009 г.

Цель   работы:   знакомство   с   нелинейными   САУ   и   методами   их исследования с помощью фазовых траекторий и припасовывания.

I. В МАТНСАD методом фазовых траекторий исследовать процесс регулирования   температуры      для   системы,   изображенной   на рисунке 1,    если    нелинейный    элемент    представляет    собой чувствительный  элемент со статической характеристикой в виде петлевой гистерезисной релейной характеристики Рис 2. Исполнительное устройство   имеет   передаточную   функцию вида:

 

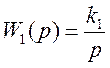
Передаточная функция ОР:

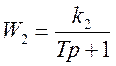
Параметры САУ:

b=1,  c=1,  k=2,  T=2

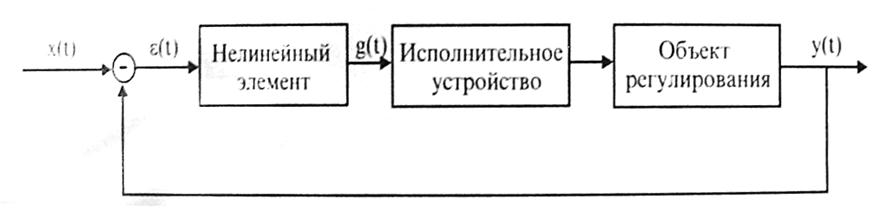
Рисунок 1.

b

c

-c

-b

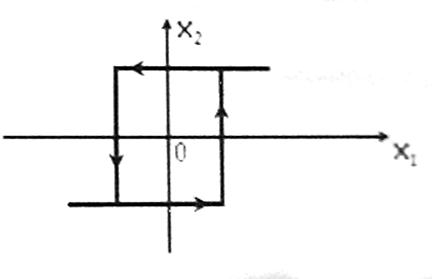
Рисунок 2

Порядок выполнения работы.

Линейная часть системы описывается уравнением:

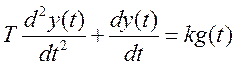
Уравнение нелинейного элемента:

Уравнение сравнивающего элемента:

. При задающем воздействии х(t)=0, получим:

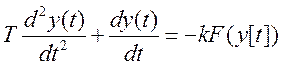
Обозначим: 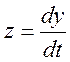, тогда: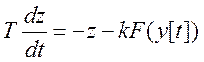        

Из рисунка 2 видно:

Если z>0, то

.

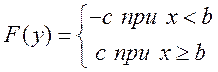Если z<0, то

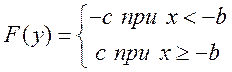
Составим программу на Mathcad:

начальные условия :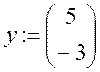 

Определим функцию D по трем линейным участкам нелинейной статической характеристики, задающую производную, приведя дифференциальное уравнение 2-го порядка к системе  2-х дифференциальных уравнений 1-го порядка:

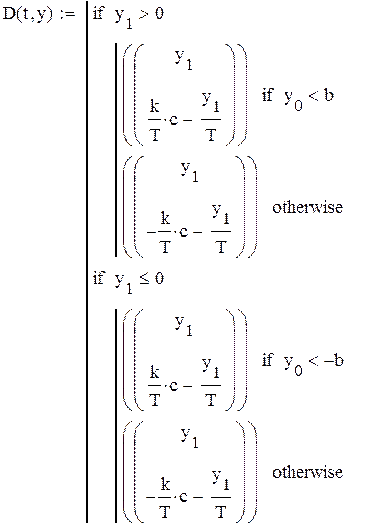
                                матрица решения:

                                           

                                           

Построим траекторию на фазовой плоскости, предполагая, что первый столбец матрицы решения Yi,₀  содержит точки в которых ищется решение дифференциального уравнения, второй Y_i,1 – содержит значения найденного решения, т.е. y(t) и третий столбец Y_i,2 содержит первые производные этого решения, т.е. dy(t)/dt.

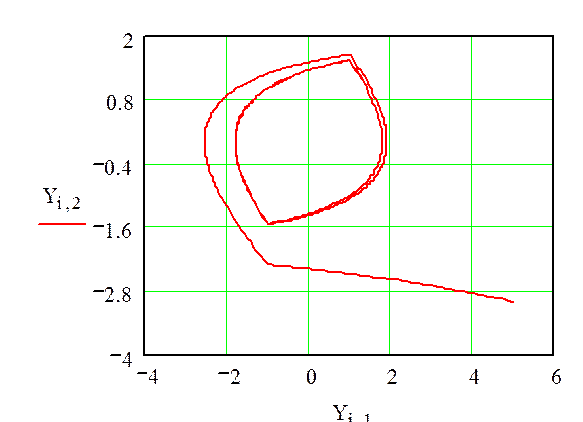
Рисунок 3 – Фазовый портрет

2. Построим фазовые траектории для различных начальных состояний.

№3

№2

№1

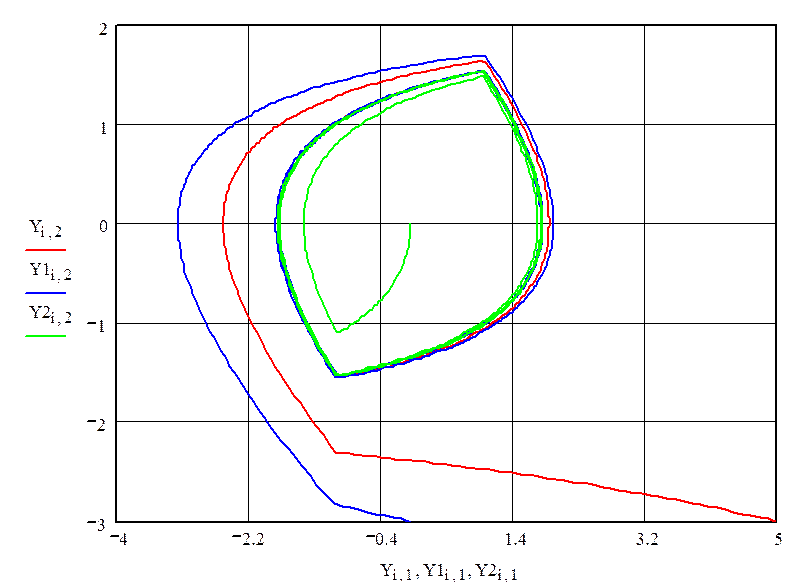
Кривая №1: Y=(5;-3)

Кривая №2: Y=(0;-3)

Кривая №3: Y=(0;0)

3. Построим переходные процессы для выходной координаты:

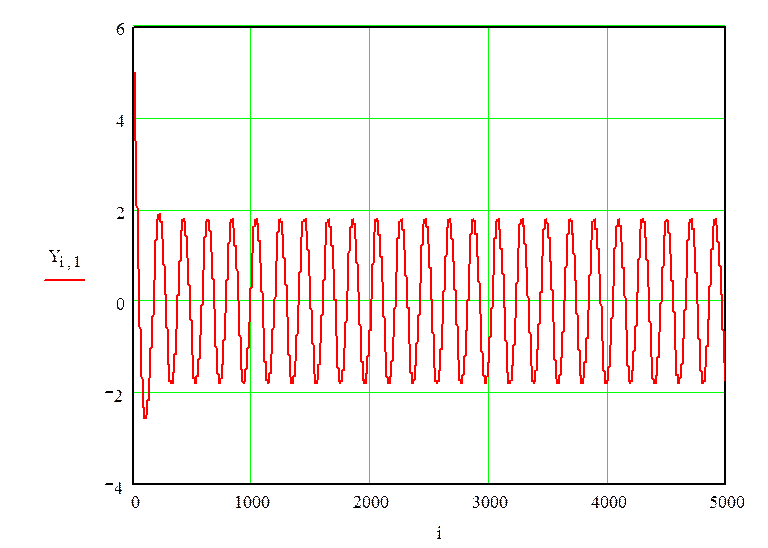
Система производит автоколебания в предельном цикле с амплитудой

Ymax=1,8  и частотой 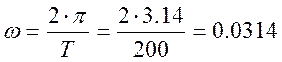сек^-1

4. Влияние параметров САУ:

При подстановки разных значений параметров, было замечено, что:

- при увеличении k, увеличивается амплитуда колебаний

- при уменьшении Т, увеличивается частота колебаний

- при увеличении b, увеличивается и амплитуда, и частота колебаний.