![]() ,
(5.13)
,
(5.13)
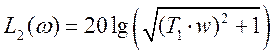 ,
(5.14)
,
(5.14)
![]() ,
(5.15)
,
(5.15)
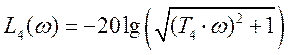 , (5.16)
, (5.16)
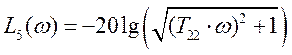 , (5.17)
, (5.17)
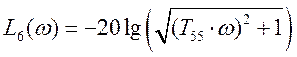 .
(5.18)
.
(5.18)
Функция Л. А. Ч. Х. разомкнутой системы:
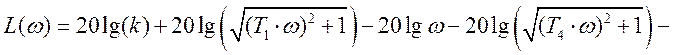
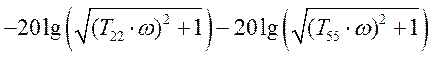 .
(5.19)
.
(5.19)
Функции Л.Ф.Ч.Х. звеньев в порядке изображения их на преобразованной структурной схеме разомкнутой САР:
![]() ,
(5.20)
,
(5.20)
![]() ,
(5.21)
,
(5.21)
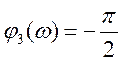 ,
(5.22)
,
(5.22)
![]() ,
(5.23)
,
(5.23)
![]() ,
(5.24)
,
(5.24)
![]() .
(5.25)
.
(5.25)
Функция Л. Ф. Ч. Х. разомкнутой системы:
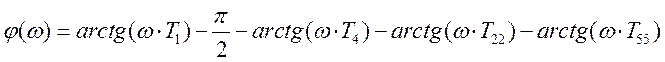 (5.26)
(5.26)
Рассчитав необходимые данные и характеристики типовых динамических звеньев, строятся Л. А. Ч. Х. и Л. Ф. Ч. Х. разомкнутой системы.
График Л.А.Ч.Х. разомкнутой системы:
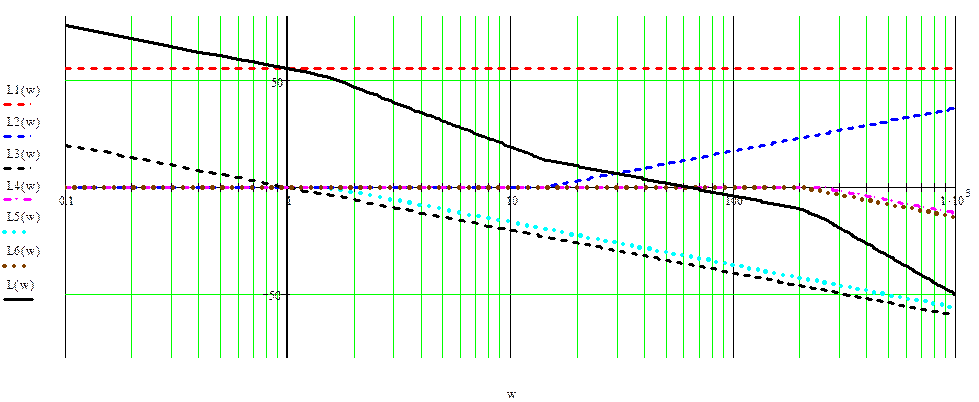
График Л.Ф.Ч.Х. разомкнутой системы:
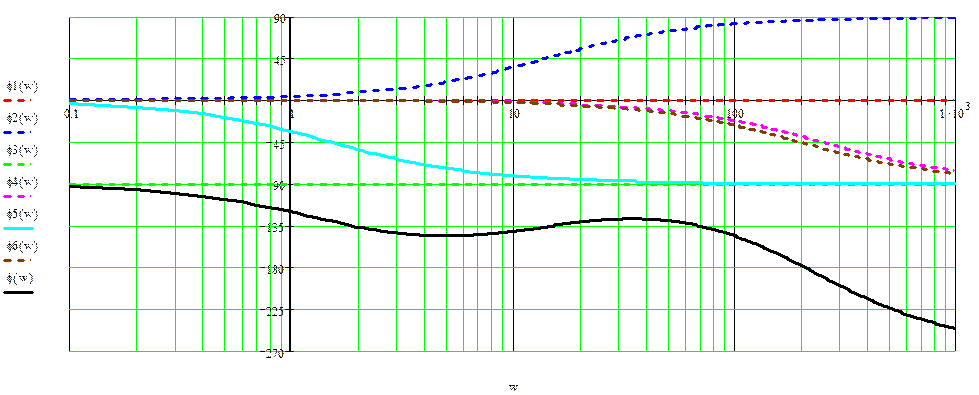
6 ПРОВЕРКА ЗАМКНУТОЙ СИСТЕМЫ НА УСТОЙЧИВОСТЬ. ОПРЕДЕЛЕНИЕ ЗАПАСА УСТОЙЧИВОСТИ ПО МОДУЛЮ И ФАЗЕ
6.1 Проверка замкнутой САР на устойчивость
Проверка САР на устойчивость будет осуществляться по критерию устойчивости Гурвица.
Передаточная функция замкнутой системы:
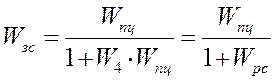 ,
(6.1)
,
(6.1)
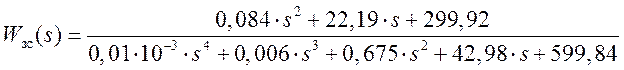 (6.2)
(6.2)
Приравняем знаменатель этого выражения к нулю, получим характеристическое уравнение замкнутой системы:
![]() (6.3)
(6.3)
Коэффициенты характеристического уравнения:
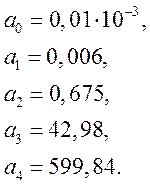
Коэффициенты характеристического уравнения положительны, значит можно рассматривать систему на устойчивость.
Критерий устойчивости системы Гурвица: Система будет устойчива, если все коэффициенты характеристического уравнения и все диагональные миноры определителя Гурвица положительны.
У нас характеристическое уравнение 4-го порядка, следовательно определитель Гурвица будет иметь вид:
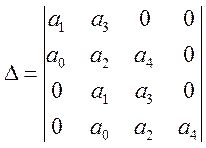 (6.4)
(6.4)
Для определения устойчивости составляем и миноры определителя:
![]() ,
(6.5)
,
(6.5)
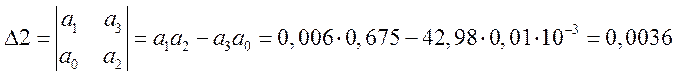 ,
(6.6)
,
(6.6)
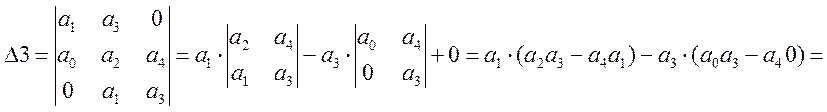
![]() , (6.7)
, (6.7)
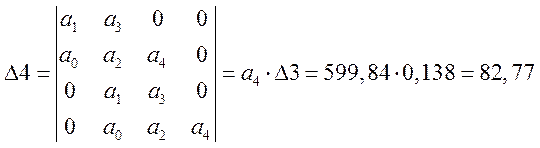 (6.8)
(6.8)
Все определители Гурвица (все n диагональные миноры матрицы) положительны, значит условие устойчивости системы по критерию Гурвица выполняется, а следовательно данная замкнутая САР устойчива.
6.2 Определение запаса устойчивости системы по фазе
Запас
устойчивости может быть определен с использованием логарифмического критерия
устойчивости Найквиста, который опирается на логарифмические характеристики
разомкнутой системы. Он гласит: система находится в устойчивом состоянии,
если частота среза меньше частоты, при которой Л.Ф.Ч.Х. переходит через угол ![]() .
.
Графики Л. А. Ч. Х. и Л. Ф. Ч. Х. разомкнутой системы.
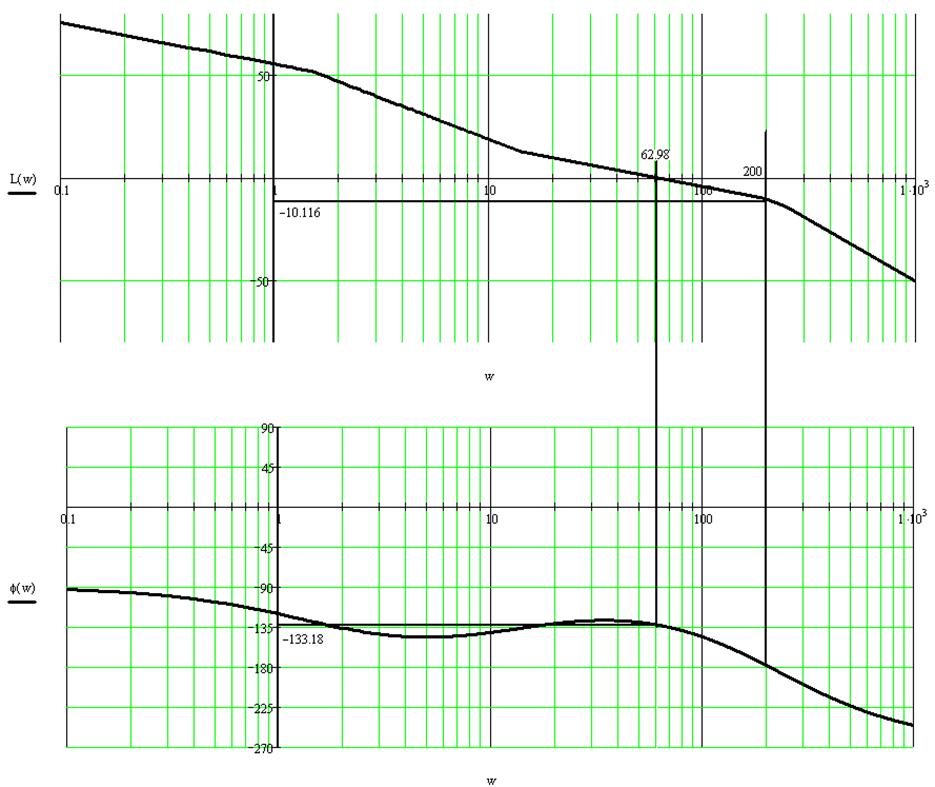
Л.А.Ч.Х. разомкнутой системы на графике пресекает ось абсцисс
при ![]()
![]() (6.9)
(6.9)
Фаза при 62,98Гц равна:
![]() .
(6.10)
.
(6.10)
Запас устойчивости по фазе:
![]() . (6.11)
. (6.11)
6.3 Определение запаса устойчивости системы по модулю
Л.Ф.Ч.Х. разомкнутой системы на графике пресекает прямую ![]() при
при ![]() .
.
![]() ,
(6.12)
,
(6.12)
![]() дБ.
(6.13)
дБ.
(6.13)
Запас устойчивости по модулю:
![]() , (6.14)
, (6.14)
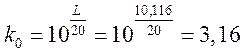 . (6.15)
. (6.15)
Т.е. можно увеличить коэффициент усиления передаточной функции в 3,16 раза.
Можно сделать вывод, что, данная система обладает запасом устойчивости как по модулю, так и по фазе.
7 РАСЧЁТ
УСТАНОВИВШЕЙСЯ ОШИБКИ СЛЕЖЕНИЯ ЗА ЗАДАЮЩИМ ВОЗДЕЙСТВИЕМ (![]() ).
).
Передаточная функция по ошибке:
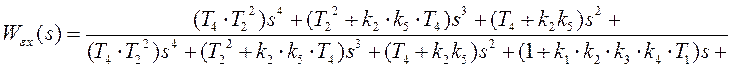
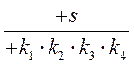 . (7.1)
. (7.1)
Входной сигнал:
![]()
![]() =100 c-1
(7.2)
=100 c-1
(7.2)
Изображение входного сигнала:
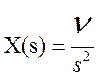 .
(7.3)
.
(7.3)
Найдём установившуюся ошибку слежения воспользовавшись теоремой об установившемся значении оригинала:
![]() , (7.4)
, (7.4)
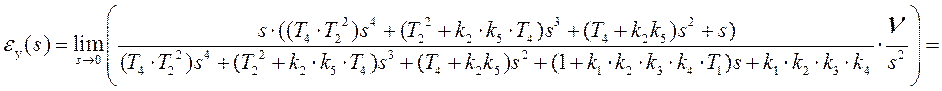
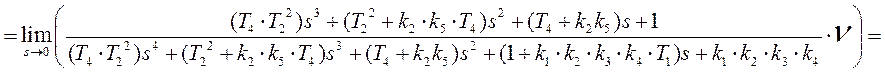
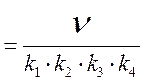 . (7.5)
. (7.5)
Установившееся значение ошибки:
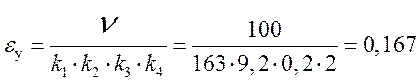 . (7.6)
. (7.6)
СПИСОК ЛИТЕРАТУРЫ
1 Юревич Е.И. Теория автоматического управления. «БХВ-Петербург», Санкт-Петербург, 2007.
2 Никулин Е.А. Основы теории автоматического управления. Частотные методы анализа и синтеза систем. «БХВ-Петербург», Санкт-Петербург, 2004.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.