Вариант 1.
Цель работы: знакомство с
нелинейными САУ и методами их исследования с помощью фазовых траекторий и
припасовывания. ![]()
![]()

Исполнительное устройство имеет передаточную функцию вида 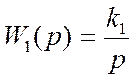
Передаточная функция объекта регулирования равна 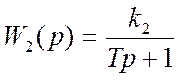
Причём ![]()
b=1 c=0.5 k=1 T=1
Нелинейный элемент представляет собой чувствительный элемент
со статической характеристикой в виде петлевой гистерезисной релейной
характеристики.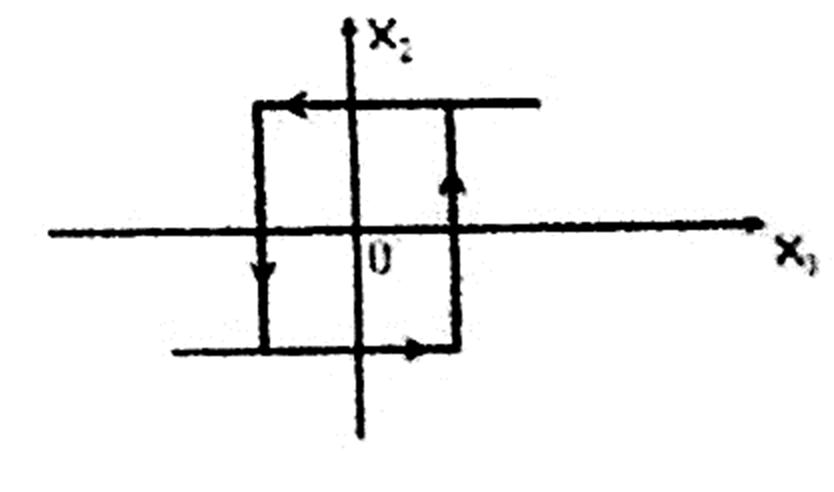
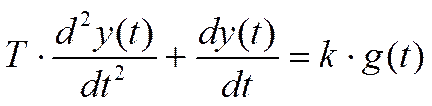
Уравнение нелинейного элемента : g(t)=F[ε(t)]
Запишем уравнение сравнивающего элемента ε(t)=x(t)-y(t)
Предположим, что задающее воздействие x(t)=0 . Тогда уравнение нелинейной САУ будет иметь вид :
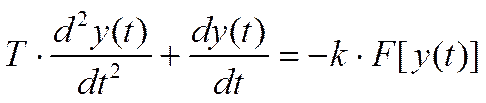
Характеристика нелинейного элемента разбивается на 2 линейных участка и для каждого из них составляется линейное дифференциальное уравнение.
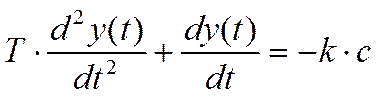
, если y>b и y>-b
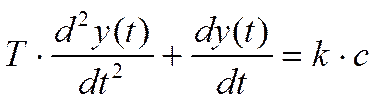 , если y<b и y<-b
, если y<b и y<-b
![]() Если
Если 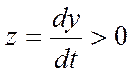 , то F(y)= -c при x<b
, то F(y)= -c при x<b
c при x>b
![]() Если
Если 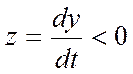 , то F(y)= -c при x<-b
, то F(y)= -c при x<-b
c при x>-b
Программа построения фазовых траекторий.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
По графику Ymax=1.1484 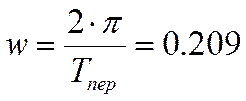
Вывод: в моём случае фазовые траектории имеют спиралевидную форму, что соответствует колебательным процессам. Расчёты показывают, что фазовые траектории образуют устойчивый предельный цикл, который соответствует устойчивым колебаниям.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.