Изображение конечных разностей функций

Изображение конечных разностей функций

Теорема 4: Пусть  является оригиналом и - ее изображением, то первая разность  также является оригиналом, и при этом справедливо равенство:

   (1)

Доказательство:

 Используя теоремы (1) и (2) и определение разности, для первой разности  получим:

Если  допускает D-преобразование, то ее разность произвольного порядка n также допускает D-преобразование, поскольку разность n-ого порядка можно представить по следующее формуле:

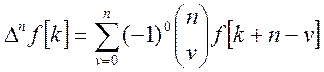
Где - факториальная функция.

N-ую разность можно представить в виде линейной комбинации решетчатых функций:

При этом могут быть получены следующие формулы с применением формулы (1):

…………………………………………………………………………….

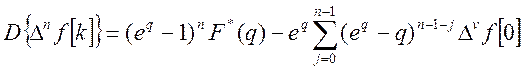   (2)

Если , то функция , и тогда получим:

   (3)