Дискретные преобразования и их основные свойства

3. Дискретные преобразования и их основные свойства

Так же как и для анализа и синтеза непрерывных систем используются различные интегральные преобразования (Лапласа, Фурье) так и для импульсных и цифровых систем применяют различные преобразования. В настоящем курсе будут рассмотрены наиболее часто используемые в практике проектирования дискретных систем автоматического преобразования

-  дискретное преобразование Лапласа;              

-  z-преобразование;

-  w-преобразование.

3.1. Дискретное преобразование Лапласа

3.1.1. Прямое D-преобразование

 Дискретное преобразование Лапласа является функциональным преобразованием решетчатых функций f[n] и определяется соотношением

                           ¥             

F*(q) =  Σ e^-qn f[n]                                                    ( 3.1 )

              n=0           

или для смещенных решетчатых функций f[n,ε]

                              ¥          

F*(q,ε) =  Σ e^-qn f[n,ε]                                               ( 3.2 )

                 n=0        

Здесь q = σ + jω - комплексное число, называемое параметром преобразования, а ε -вещественный параметр. Если сравнить (3.1) или (3.2) с определением обычного преобразования Лапласа функции f(t)

                          ¥              

F(q) =   ∫ e^-st f(t)dt                                                      ( 3.3 )

 0               

то легко заметить аналогию между ними. Интегралу с бесконечным пределом соответствует бесконечная сумма - ряд в (3.1) или в (3.2); непрерывной переменной t -дискретная переменная n и, наконец, произвольной непрерывной функции f(t) - решетчатая функция f[n] или смещенная решетчатая функция f[n,ε].

Параметр q связан с параметром s соотношением

            q = sT,

где Т – период квантования непрерывной функции идеальным импульсным элементом.

Соотношение (3.2) устанавливает соответствие между решетчатой функцией f[n,ε] и функцией F*(q,ε) комплексной переменной q. По аналогии с обычным преобразованием Лапласа  функ­цию f[n,ε] называют оригиналом, а F*(q,ε)  - изображением. Само преобразование функции f[n,ε] в F*(q,ε) называют прямым D-преобразованием.

Так как параметр ε не влияет на свойства D-преобразования, то для упрощения записи  в основном будем рассматривать решетчатую функцию f[n], а не смещенную решетчатую функцию f[n,ε].

Для того чтобы изображение решетчатой функции было определено, ряд (3.1) должен быть сходящимся. Значение величины σ_с, для которого при σ > σ_с ряд (3.1) сходится, а при σ < σ_с расходится, называется абсциссой сходимости. Абсцисса сходимости σ_с представляет, таким образом, наибольшую нижнюю границу значений σ₀, при которых ряд (3.1) сходится.

Если для данной решетчатой функции f[n] абсцисса сходимости σ_с < :, то ряд (3.1) сходится при всех значениях q, удовлетворяющих условию Re q = σ > σ_с. В этом случае функция f[n] называется преобразуемой. Всякой преобразуемой функции f[n] соответствует изображение F*(q).

Если же для данной решетчатой функции f[n] абсцисса сходимости  σ_с = +:, то ряд (3.1) расходится при любом q. В этом случае изображение для f[n] не существует.

Пример 1. Пусть f[n] = 1[n], как показано на рис. 3.1. Изображение «постоянной» решетчатой функции равно при Re q > 0:

                           ¥                           1          e^q

F*(q) =  Σ e^-qn 1[n] = —— = —— .                                    

              n=0                      1-e^-q     e^q -1

Пример 2. Пусть f[n,ε] = e^α(n+ε), где α – вещественное число. Такая решетчатая функция при α < 0 и α > 0 показана на рис. 3.2. Изображение решетчатой экспоненты равно

                           ¥                                    e^αε           e^q e^αε

F*(q) =  Σ e^-qn e^αn e^αε   = ———— = ——— .

              n=0                               1- e^{-(q – α)}       e^q - e^αε

при ε = 0 получаем

                                                 e^q

F*(q) =  D{e^αn }  =  ——— .

                                    e^q - e^α

Суммирование здесь возможно при Re q > α. В этом случае абсцисса сходимости σ_с = α.

Рис. 3.2. Смещенные решетчатые экспоненциальные функции

Пример 3. Пусть f[n] = n! или f[n] = e^αn2.

Изображений этих функций не существует, так как для них абсцисса сходимости σ_с равна бесконечности.

Таким образом, существование абсциссы сходимости 0<s_с, < со обеспечивает существование изображения. Если решетчатая функция удовлетворяет условию

|f[n]| < M e^α_—ⁿ,

т. е. если порядок роста ее не больше, чем порядок роста e^α_—ⁿ, то абсцисса сходимости      σ < σ_с  и, следовательно, изображение этой функции существует.

Из определения D-преобразования (3.1) или (3.2) и приведенных выше примеров видно, что изображения решетчатых функций являются функциями e^q. Это характерное свойство дискретного преобразова­ния Лапласа. Для того чтобы подчеркнуть это обстоятельство и отличать изображение решетчатой функции (3.1) от изображения соот­ветствующей непрерывной функции (3.3). обозначение первого изображения снабжено звездочкой.

Рассмотрим теперь F*(q) на плоскости комплексной переменной q. Так как F*(q) является функцией e^q , а e^q представляет собой перио­дическую функцию вдоль мнимой оси jω (e^q+2kπj = e^q ) то и F*(q) -  также периодическая функция вдоль мнимой оси, т. е.

F*(q) = F*(q+2πkj),                                                              (3.4)

и  изображения  решетчатых функций полностью определяются при Re q > σ_с в любой полосе, параллельной действии тельной оси и шириной 2π. Целесообразно поэтому выбрать полосу симметричной относи­тельно действительной оси. т. е. так, чтобы

- π < Im q £ π,

как это показано на рис. 3.3. В полуполосе Req > σ_сизображениеF*(q) является аналитическойфункцией e^q и q. Во многих случаях F*(q) может быть аналитически продолжена в левую полуполосу Re q < σ_с. 

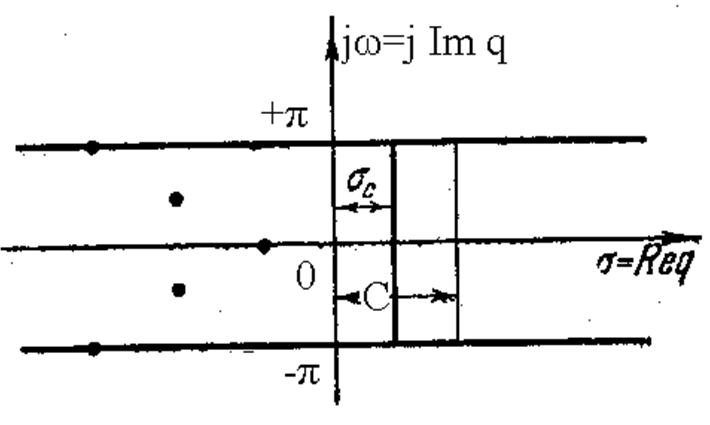
Рис. 3.3. Плоскость комплексной переменной q. Полоса - π < Imq£π.

В общем случае F*(q) внутри полосы может иметь особые точки при Re q < σ_с, например полюсы, в которых F*(q) обращается в бесконечность. В полосе - π < Im q £ π каждому комплексному полюсу q_ν = σ_ν + jω соответствует обязательно сопряженный полюс q_ν+1 = σ_ν+1 - jω так как коэффициенты, входящие в F*(q), в случае действительной f[n] всегда вещественны. Это обстоятельство и является причиной выбора именно этой полосы. Во всех остальных полосах мнимые части этих полюсов отличаются на величину ±2πkj. Если q_{ν, ν+1} = σ_ν ± jπ,  т.е. ω _ν = π, то полюсы лежат на границах полосы. В этом случае нужно учитывать один из этих полюсов, например  q_ν = σ_ν + jω (рис. 3.3). В дальнейшем, говоря об особых точках q изображения F*(q) будем иметь в виду особые точки, лежащие в основной полосе, не оговаривая этого каждый раз.

Если решетчатая функция f[n] преобразуема, то F*(q) при Re q / σ_с  является единственным изображением f[n] и обратно, изображению F*(q) соответствует при n / 0 единственная решетчатая функция f[n]. Таким образом, соответствие между оригиналом f[n] и изображением F*(q) при этих условиях однозначно.