Дискретные преобразования и их основные свойства, страница 2

В ряде случаев, например при рассмотрении стационарных регулярных и случайных воздействий, нужно рассматривать значения решетчатой функции не только при n /0, но и при n < 0. Для таких решетчатых функций используется двустороннее D-преобразование, определяемое соотношением

                           ¥             

F*(q) =  Σ   e^-qn f[n]                                                  ( 3.5 )

             n=-¥

Если f[n] º 0 при n < 0, то двустороннее D-преобразование сводится к одностороннему.

3.1.2. Обратное D-преобразование

Прямое D-преобразование решает задачу определения изображения F*(q)  или F*(q,ε) по оригиналу f[n] или f[n,ε]. Решение обратной задачи сводится к определению оригинала f[n] или f[n,ε] по изображению F*(q)  или F*(q,ε). Преобразование изображения в оригинал называется обратным D-преобразованием, или кратко D^-1-преобразованием. Известны выражения, называемые формулами обращения, для нахождения несмещенных и смещенных решетчатых функций по их изображениям (см. формулы (3.5) и (3.6)).

	(3.6)
	(3.7)

Обратное двустороннее D-преобразование может быть определено таким же  путем, как и одностороннее D^-1-преобразование:

(3.8)

На практике формулами (3.1), (3.2) и (3.6), (3.7) пользоваться не удобно, поэтому используются специальные таблицы дискретного преобразования Лапласа (см., например табл. 3.1)

Оригиналы и их изображения для дискретного преобразования Лапласа     Таблица 3.

№	оригинал	изображение	№	оригинал	Изображение
1	1[n]		7
2	ean		8
3			9
4			10	nean
5	n		11
6	n2		12

3.1.3. Основные теоремы и правила D-преобразования

Важную роль при использовании дискретного преобразования Лапласа играют правила и теоремы, которые устанавливают соответствие между операциями, производимыми в области оригиналов и изображений. Эти правила и теоремы дают возможность весьма просто, минуя непосредственное суммирование, которое зачастую оказывается затруднительным, найти изображение многих решетчатых функций. Кроме того, они позволяют применить дискретное преобразование Лапласа к решению разностных уравнений и к исследованию установившихся и переходных процессов в импульсных системах.

Теорема 1. Линейность оригиналов и изображений

Если для решетчатых функций f_n[n] , где n = 1, 2, … определены их изображения

D{f_n[n]} = F*_n(q),

то для решетчатой функции

                         k                

f[n] =   Σ a_nf_n[n]                                                        

n=1             

изображение F*(q) может быть найдено как

                           k              

F*(q) =  Σ a_nF*_n(q).                                                              ( 3.9 )

              n=1           

Пример 1.

            Пусть Так как 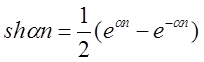, то на основании теоремы 1 имеем

учитывая, что                                                     e^q

D{e^αn }  =  ——— ,

                                    e^q - e^α

получаем

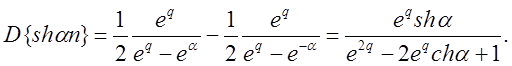
Теорема 2. Смещение аргумента в области оригиналов (теорема сдвига).

· Пусть D{f[n]} = F*(q). Тогда

                                                                    k-1                  

D{f[n+k]} =   e^qk [F*(q) - Σ e^-qr f [r]]                                 (3.10)                                                                                                 r=1             

В частном случае, если  f[0] = f[1] = … = f[k-1] = 0, то

D{f[n+k]} =   e^qk F*(q).                                                        (3.11)

· Для решетчатой функции f[n-k] справедливо следующее соотношение:

                                                                     k                   

D{f[n-k]} =   e^-qk [F*(q) + Σ e^qr f [-r]]                               (3.12)                                                                                                  r=1             

В частном случае, когда f[-1] = f[-2] = … = f[-k] = 0, получаем:

D{f[n-k]} =   e^-qk F*(q).                                                        (3.13)

Пример 2. Найти изображение запаздывающей постоянной решетчатой функции

f{n} = 1[n-k], f[n] º 0 при n< k.

Принимая во внимание, что

                                     e^q

D{1[n] }  =  ——— ,

                                    e^q - 1

согласно теореме смещения аргумента получаем

 e^q                    1

D{1[n-k]} = e^-qk   ———  = ——————,

            e^q – 1      (e^q – 1) e^q(k-1)

при k=1 имеем

               1

D{1[n-1]} =   ———.

e^q – 1      

Теорема 3. Смещение независимого переменного в области изображения (теорема смещения).

                        F*(q6l) = D{e^7lnf[n]}.                                                          (3.14)