f[0,e] = lim F*(q,e). (3.21)
q":
Пример 8.
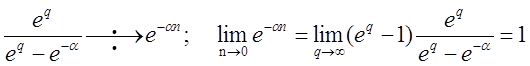
Из теоремы о начальном значении следует, что если изображение F*(q) правильно, т. е. степень числителя меньше степени знаменателя, то
f[0] = lim F*(q) = 0.
q"¥
Иными словами, решетчатая функция, соответствующая правильному изображению, равна нулю в начальный момент времени.
Установленные правила и теоремы являются основой D-преобразования. Ценность их состоит не только в том, что при их помощи можно увеличить количество соответствий между оригиналами и изображениями, но и в том, что используя их, можно исследовать свойства оригиналов при помощи изображений, получение которых для многих задач не представляет никаких трудностей.
3.1.4. Связь между изображениями непрерывной функции и соответствующей ей решетчатой функции. D-преобразование
В этом разделе будет указана связь между изображениями решетчатой и соответствующей ей непрерывной функций. Эта связь дает возможность по изображениям обычного преобразования Лапласа определить изображение дискретного преобразования Лапласа и обратно, а также установить соответствие операций над этими изображениями.
Рассмотрим непрерывную функцию fT(Tt) = f(t)аргумента t = t/T, определенную в интервале 0 < t < :. Изображение этой функции в смысле непрерывного преобразования Лапласа равно
:
F(q) = L{f(t)} = ∫ e-st f(t)dt , ( 3.22 )
0
где q = sT – параметр преобразования и
1 q
F(q) = — FT(—).
T T
Смещенная решетчатая функция f[n,ε] = f(n+ε) получается из непрерывной функции f(t) заменой в последней переменной t на n+ε. Дискреты смещенной решетчатой функции сдвинуты по отношению к f[n,0] = f[n] при ε > 0 вправо. Изображение этой смещенной решетчатой функции в смысле D-преобразования равно
:
F*(q, ε) = D{f[n, ε ]} = Σ e-qn f[n, ε],
n=0
где ε рассматривается как параметр. В частности, при ε = 0 получаем
:
F*(q, 0) = D{f[n, 0]} = Σ e-qn f[n, 0],
n=0
или проще:
:
F*(q) = D{f[n]} = Σ e-qn f[n].
n=0
Связь между изображением решетчатой функции F*(q, ε) и изображением F(q) соответствующей непрерывной функции определяется соотношением
:
F*(q, ε) = Σ e(q+2πjr)ε F(q+2πjr), (3.33)
r = -:
где ε изменяется в интервале 0 < ε £ 1.
При ε =0 соотношение (3.33) принимает вид
1 :
F*(q) = — f[0] + Σ F(q+2πjr), (3.34)
2 r = -:
То обстоятельство, что из соотношения (3.33) не следует соотношение (3.34) при ε = 0, если только f[0] ¹ 0, связано с известным свойством рядов Фурье, состоящим в том, что сумма ряда Фурье в точке разрыва первого рода равна среднему арифметическому значению функции справа и слева от точки разрыва.
Соотношения (3.33) и (3.34) позволяют по изображению F(q) непрерывной функции f(t) найти изображение F*(q, ε) соответствующей решетчатой функции f[n, ε] при любом фиксированном значении ε. Соотношения (3.33) или (3.34), связывающие изображения непрерывной и решетчатой функций, можно рассматривать как преобразование, устанавливающее соответствие между этими изображениями.
Обозначив операцию этого преобразования через D{F(q)} запишем (3.33) в виде
:
F*(q, ε) = D{F(q)} = Σ e(q+2πjr)ε F(q+2πjr), (3.35) r = -:
Выражение (3.35) определяет прямое D-преобразование. D-преобразование и D-преобразование связаны между собой соотношением
D{ f[n, ε] } = D{L{f(t)}}.
Пример 9.Рассмотрим единичную ступенчатую функцию f(t) = 1(t).Её изображение
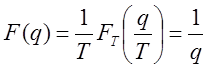
согласно (3.34) получаем
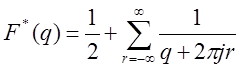
С другой стороны, известно, что
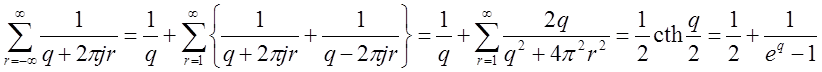
Следовательно,
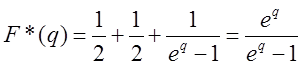
Последний результат совпадает с результатом, полученным в примере №1 раздела 3.1.1.
Рассмотрим теперь вопрос об установлении физического смысла D-преобразования. Для этого от изображений перейдем к спектрам непрерывной F(jv) и решетчатой F(jv,e) функций. Имеем следующее соотношение:
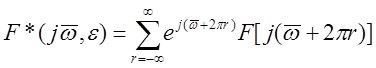
для e = 0 имеем также
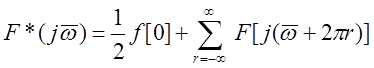
Из последнего соотношения следует, что спектр F(jv) решетчатой функции f[n] равен с точностью до постоянного слагаемого 1/2f[0] сумме спектров соответствующей непрерывной функции, смещенных по оси частот на величины 2pr, где r изменяется от - ¥ до +¥.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.