Теорема смещения является теоремой двойственности для теоремы сдвига. В этих теоремах операции в области оригиналов и изображений поменялись местами.
Пример 3. Найдем изображение решетчатой функции f[n] = elnsh an
Воспользовавшись изображением sh an, получаем на основании теоремы смещения:
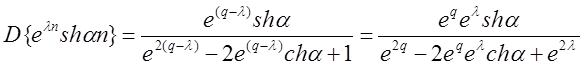
Теорема 3. Изображение разностей.
Для первой разности решетчатой функции
Δf[n] = f[n+1] – f[n]
на основании теорем линейности и сдвига получаем
D{Δf[n]} = (eq – 1)F*(q) - eq f[0] (3.15)
Для второй разности решетчатой функции
Δ2f[n] = Δf[n+1] – Δf[n]
На основании теоремы сдвига и соотношения (3.15) после преобразования получаем
D{Δ2f[n]} = (eq – 1)2F*(q) - eq (eq -1)f[0] - eq Δf[0] (3.16)
Для k-ой разности решетчатой функции получается следующее выражение:
k-1
D{ Δkf[n]} = (eq – 1)k F*(q) + eq Σ (eq – 1)k-1-r Δrf[0] (3.17) r=1
Здесь нужно считать Δ0f[0] = f[0].
Пример 4. Найдем изображение первой разности экспоненциальной решетчатой функции f[n] = ean. По формуле (3.15) получаем:
eq eq(ea – 1)
D{Dean} = (eq –1) ———— - e-q = ————.
eq – ea eq – ea
Теорема 4. Изображение суммы
Рассмотрим функцию, определяющую сумму решетчатой функции:
n-1
f[n] = Σ f[m]
m=0
Изображение разности функции f[n] в соответствии с предыдущей теоремой равно:
n-1 n-1
D{D Σ f[m] } = D{f[n]} = (eq -1) D{D Σ f[m] },
m=0 m=0
так как значение суммы при n = 0 равно нулю. Следовательно, изображение от суммы решетчатой функции f[m] определяется как
n-1 F*(q)
D{DΣ f[m] } = ———. (3.18)
m=0 eq – 1
Пример 5. Найдем оригинал, соответствующий изображению
eq
F*(q) = ———————.
(eq – 1)(eq – ea)
замечая, что
eq
F*(q) = ——— = D{ ean},
(eq – ea)
находим согласно теореме о сумме решетчатой функции
F*(q) n-1
——— = D{Σ eam }.
eq – 1 m=0
Но
n-1 ean -1
Σ eam = ——— ,
m=0 ea -1
следовательно,
eq 1 - ean
F*(q) = ——————— = D{ ——— }.
(eq – 1)(eq – ea) 1 - ea
Найденная решетчатая функция показана на рис. 3.4 для a = -0,5 и a = 0,5.
|
|
|
Рис. 3.4. Решетчатая функция в примере 5.
Примеры применения теорем об изображении разностей и сумм показывают, что множитель (еq— 1) в дискретном преобразовании Лапласа играет роль параметра преобразования q или s в обычном преобразовании Лапласа, и устанавливают связь формального операторного метода в теории разностных уравнений с дискретным преобразованием Лапласа.
Эти свойства наряду с теоремой сдвига лежат в основе метода решения линейных разностных уравнений.
Теорема 5. Умножение изображений (теорема свертывания в вещественной области).
Эта теорема является одной из наиболее важных для приложений теорем. Она дает возможность найти оригинал произведения изображений, если известны оригиналы сомножителей.
Пусть
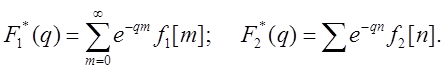
Образуем произведение
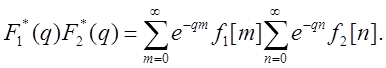
Произведя перемножение рядов в правой части равенства при Re q > sc, где sc - наибольшая из абсцисс сходимости, получим:
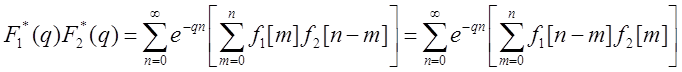
так как при n < m решетчатые функции равны нулю.
Согласно определению D-преобразования получаем
|
|
(3.19) |
Эти формулы называются формулами свертывания в вещественной области.
Теорема 6. Конечное значение решетчатой функции (теорема о конечном значении). Теорема устанавливает соотношение между изображением и конечным значением решетчатой функции.
Для несмещенной решетчатой функции справедливо следующее соотношение:
lim f[n] = lim (eq – 1)F*(q). (3.20)
n": q"0
аналогично для смещенной решетчатой функции:
lim f[n,e] = lim (eq – 1)F*(q,e). (3.21)
n": q"0
Пример 6.
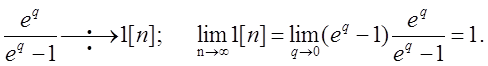
Пример 7.
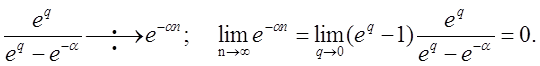
Теорема 7. Начальное значение решетчатой функции (теорема о начальном значении).
Для несмещенной решетчатой функции справедливо следующее соотношение:
f[0] = lim f[n] = lim (1 - e-q)F*(q) = lim F*(q), (3.22)
n"0q"¥ q"¥
аналогичное соотношение для смещенной решетчатой функции:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.