Анализ устойчивости по критерию Найквиста с помощью ЛАФЧХ: Методическое пособие к практическим работам

Международный Университет

      Бизнеса и Управления

                                                      БАЛАКОВСКИЙ

        ИНСТИТУТ

БИЗНЕСА И УПРАВЛЕНИЯ

ПРАКТИЧЕСКАЯ РАБОТА 

«АНАЛИЗ УСТОЙЧИВОСТИ ПО КРИТЕРИЮ НАЙКВИСТА С ПОМОЩЬЮ ЛАФЧХ»

Методическое пособие к практическим работам  по курсу: «Теория автоматического управления»

для студентов специальностей 210100 – «Управление и информатика в технических системах»

230700 – «Сервис», 351400 – «Прикладная информатика»,

Одобрено

Редакционно-издательским

советом

Балаковского Института

Бизнеса и Управления

Балаково 2004

ЦЕЛЬ РАБОТЫ: научиться строить асимптотическую ЛАФЧХ разомкнутой САУ и определять се устойчивость по критерию Найквиста.

ТЕОРИТИЧЕСКИЕ ПОЛОЖЕНИЯ

В данной работе исследуется устойчивость наиболее распространенной САУ - системы с обратной связью или замкнутой системы. Эта система более склонна к неустойчивой работе, так как на вход этой системы поступает два сигнала: управляющий сигнал U(t) и сигнал обратной связи Xoc(t). (Рисунок 3.1)

Построение системы координат

По оси абсцисс в логарифмическом масштабе откладываются знамения частот. Принимаем,что и точке пересечения оси абсцисс и ординат =1 (или 1 герц), тогда lg=0

Определим lg при различных :

Определяем lg при <0 следующим образом

Аналогично определяются lgдля других частот. По этим даyным вид­но, что при увеличении  в 10 раз lg увеличивается на 1 единицу, при уменьшении  в 10 раз, lg уменьшается на единицу. Эта величина называ­ется ДЕКАДОЙ. если построение ЛАЧХ ведется в тетрадке, разлинованную в клетку, то масштаб удобно взять следующий: одна декада равна 0 клеткам (рисунок 3.2).

Начиная с точки пересечения осей координат ,где принимаем  = 1 (lg 1 = 0) вправо через 3 клетки отмечаем = 2, через 6 клеток  = 4, через 7,8 клеток = 6, через 9.0 клеток = 8 и через 10 клеток  = 10. Особен­ность такого построения в том, что масштаб берется логарифмический, со­гласно расчета Ig , а по оси абсцисс записываются действительные значе­ния . Далее, аналогично отмечаем другие значения lg. Через 13 клеток (относительно начала координат)  = 20, через 16 клеток  =40, через 17,8 клеток  = 80 и т. д.

Масштабирование оси абсцисс при < 1 проводим следующим обра­зом. Через 10 клеток влево относительно начала координат откладываем =0.1. Затем, двигаясь   вправо   от   этой точки через 3 клетки, отмечаем =0.2, через 6   клеток = 0.4 и т.д. Затем, через 20 клеток влево (относи­тельно начала координат) откладываем = 0.01. Снова двигаясь вправо че­рез 3 клетки =0.02, через 6 клеток 0.04 и т.д. Таким образом, масштабиро­вание оси абсцисс в пределах декады проводится одинаково. Разница в том, относительно какой точки начинаем двигаться вправо. Так, если относитель­но =10, то далее вправо 20, 40, 60, 80. Если относительно =0.1, то далее вправо 0.2, 0.4, 0.6, 0.8. Такой способ масштабирования оси абсцисс намного проще, по сравнению с вычислением логарифма каждого значения и откла­дывание его в логарифмическом масштабе на оси абсцисс.

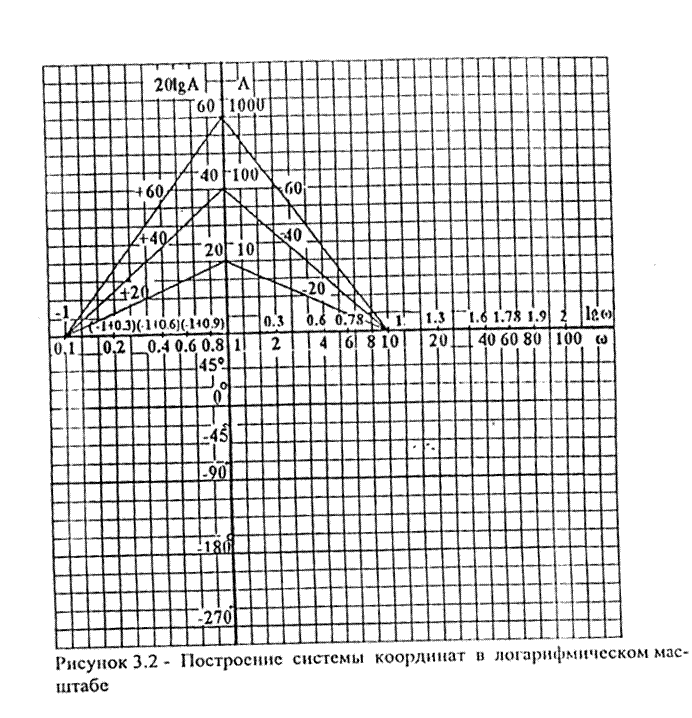По оси ординат показывается знамение коэффициента усиления или значение амплитуды и тоже в логарифмическоммасштабе, точнее 20 IgA(или в децибелах)

Если построение ЛАЧХ ведется в тетрадке в клетку, то масштаб удоб­но взять 20 дБ = 4 клетки. Теперь, согласно выбранному масштабу, по оси абсцисс и по оси ординат необходимо определить наклон ЛАЧХ. Известно, что асимптотическая ЛАХ апериодического звена после =1/Т имеет наклон -20 дБ/дек, а колебательного звена -40 дБ/дек. Для получения вели­чины этого наклона из точки на оси ординат равной 20 дБ проводим прямую до точки на оси абсцисс равной =10 (или 1 декада). Получим отрезок пря­мой с наклоном -20 дБ/сек. Если из точки на оси ординат равной 40 дБ про­вести прямую в точку па оси абсцисс равной со = 10, то получим отрезок с наклоном -40 дБ/дек. Если в эту же точку (=10 провести прямую из точки на оси ординат равной 60дБ, то получим отрезок с наклоном -60 дБ/дек и т.д. Для получения положительного наклона проведем прямую из точки  = 0.1 на оси абсцисс до точки 20 lgA = +20дБ на оси ординат. Для получения

наклона +40 дБ/дек проводим прямую из точки =0.1 до точки 20 IgA = +40 дБ и т.д.

Для построения фазовой логарифмической характеристики на оси ор­динат ниже точки 0 отложим 4 клетки (2 см) и проведем дополнительную ось абсцисс параллельно построенной и с таким же логарифмическим масшта­бом частот. Принимаем, что в точке пересечения осей φ=0, тогда через 4 клетки вниз (если построение ведется в тетрадке в клетку) по оси ординат откладываем -90, еще через 4 клетки -180 и т.д.

Если относительно (φ=0,чсрез 4 клетки вверх (или через 2 см.) отло­жить точку, то она соответствует углу равному +90. Через эти точки прово­дим прямые параллельно оси абсцисс для удобства построения фазовой ло­гарифмической характеристики. Таким образом, система координат для по­строения ЛАХ и ЛФХ готова.

Построение логарифмической амплитудной характеристики

В инженерных расчетах для существенного упрощения процесса по­строения ЛАХ действительную ЛАХ заменяют приближенной (аcсиметрической), в которой криволинейныеучастки ЛАХ представляют в виде прямых линий. При этом максимальное  расхождение возникает при собственных частотах звена ( =1/Т) и равны = 20 lg 2 = 3 дБ., что вполне допустимо, учитывая точность, получения самой математической модели САУ.

Построение асимптотической ЛАХ всегда начинают с определения собственной или сопрягаемой частоты каждого звена =1/Т,где Т - посто­янная времени этого звена. Значения этих частот откладываем на оси абс­цисс и  эти точки проводим вертикальные штриховые линии (рисунок З.З) тем определяется общин коэффициент усиления системы K_0бщ=K₁ ...К и вычисляется 20 IgK_0бщ.Переходим непосредственно к по­строению АХ.

Если в САУ пет интегрирующего звена, то ЛАХ низких частот пред­ставляет собой прямую линию параллельную оси абсцисс с ординатой рав­ной 20lg K_0бщ  до первой сопрягаемой частоты . После этой сопрягаемой частоты наклон -20дБ/дек, если это было апериодическое звено или -40дБ/дек, если это колебательное звено. Так, после каждой следующей со­прягаемой частоты, наклон ЛАХ меняется в зависимости от вида этого звена. Если, например, согласно рисунку 3.3  соответствует апериодическому звену,  - колебательному,  - форсирующему, а интегрирующего звена нет, то  наклон асимптотической ЛАХ будет меняться следующим образом: до  - прямая, наклон 0 дБ/дек с ординатой20 IgK_{0бщ .}После  до  наклон -20 дБ/дек, соответствует апериодическому звену. После до  наклон -60 дБ/дек (колебательное звено увеличило наклон сразу на -40 дБ/дек ), после и далее наклон -40 дБ/дек (форсирующее звено уменьши­ло наклон на +20 дБ/дек).