Если а САУ есть интегрирующее звено, то вначале построения можно провести без его учета (как показано выше), а после окончания такого построения честь влияние интегрирующего звена. Для этого ЛАХ интегрирующего звона представить в виде
![]()
К - коэффициент усиления
интегрирующего звена, который раньше был учтен при построении ЛАХ без
интегрирующего звена. Второе слагаемое -20 lg![]() показывает наклон ЛАХ интегрирующего звена
20 дБ/дек одинаковый на всех частотах.
показывает наклон ЛАХ интегрирующего звена
20 дБ/дек одинаковый на всех частотах.
Построение
ЛАХ с интегрирующим звеном производится следующим образом. Через начало координат
проводится прямая с наклоном -20 дБ/дек. При ![]() =1 (на оси ординат) ЛАХ с интегрирующим
звеном и без него совпадают (точка N ).При
=1 (на оси ординат) ЛАХ с интегрирующим
звеном и без него совпадают (точка N ).При ![]() <1 интегрирующее звено
„приподнимает" ЛАХ и при
<1 интегрирующее звено
„приподнимает" ЛАХ и при ![]() <<1 ЛАХ идет вверх с наклоном
-20дБ/дек (отрезок МК ). При
<<1 ЛАХ идет вверх с наклоном
-20дБ/дек (отрезок МК ). При ![]() >1 интегрирующее звено „опускает"
ЛАХ и на каждом отрезке асимптотически построенной
>1 интегрирующее звено „опускает"
ЛАХ и на каждом отрезке асимптотически построенной
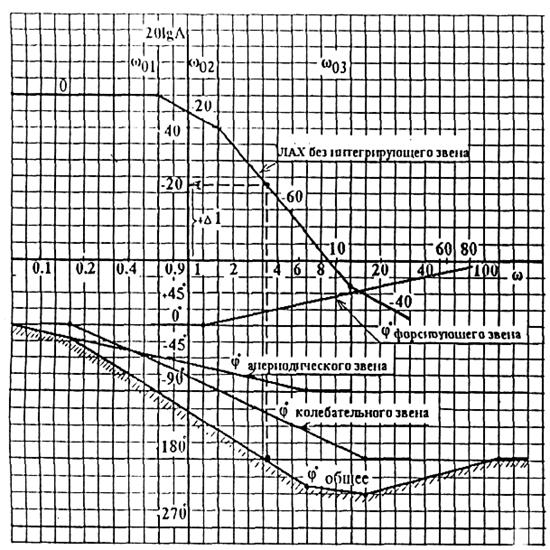 Рисунок 3.3 - Построение асимптотической
ЛАХ и ЛФХ без интегрирующего звена
Рисунок 3.3 - Построение асимптотической
ЛАХ и ЛФХ без интегрирующего звена
![]() - собственная частота
апериодического звена
- собственная частота
апериодического звена
![]() - собственная частота
колебательного звена
- собственная частота
колебательного звена
![]() - собственная частота форсирующего
звена
- собственная частота форсирующего
звена
ЛАХ без интегрирующего звена этот наклон увеличивается дополнительно на -20дБ/дек. В результате ось абсцисс будет пересечена при меньшой частоте (точка L на рисунке 3.4)
Построение логарифмической фазовой характеристики
ЛФХ характеризует угол отставания выходного сигнала САУ от входного в зависимости от частоты входного сигнала. Для дифференцирующего и форсирующего звена ЛФХ проходит с опережением выходного сигнала, но в любой реальном САУ состоящей из различных звеньев на ее выходе всегда будет отставание выходного сигнала. Рассмотрим способ асимптотического построения логарифмической
фазочастотной характеристики
апериодического звена, т.е. путем замены действительной кривой ЛФХ прямыми
линиями. При собственной частоте![]() = 1/7 угол отставания апериодического звена
= 1/7 угол отставания апериодического звена
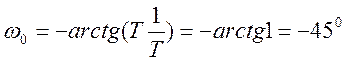
Если частота
увеличивается на 1 декаду в секунду (в 10 раз ) Относительно собственной
частоты ![]() ,
то
,
то
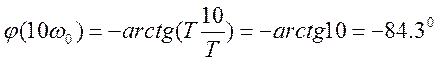 Для упрощения построения ЛФХ
принимаем
Для упрощения построения ЛФХ
принимаем ![]() .
.
Если частота
уменьшится на 1 декаду относительно ![]() , то
, то 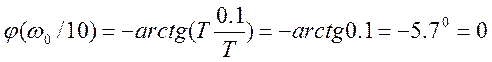
Исходя из этого, асимптотическое построение логарифмической фазочастотной характеристики апериодического звена проводим в следующей последовательности.
Определяем ![]() начала и конца фазовой
характеристики апериодического звена
начала и конца фазовой
характеристики апериодического звена
- при ![]()
![]()
- при ![]()
![]()
- при ![]()
![]()
Через эти точки проводим
прямую. При других значениях ![]() фазовая характеристика апериодического звена
выглядит следующим образом:
фазовая характеристика апериодического звена
выглядит следующим образом:
- при ![]()
![]()
- при ![]()
![]()
Асимптотическое построение фазочастотной характеристики колебательного звена проводится аналогично
- ![]()
- ![]() ;
; ![]() ;
;
- ![]() ;
;
С учетом этого, фазочастотная характеристика колебательного звена строится в следующей последовательности.
- при ![]()
![]() ;
;
- при ![]()
![]() ;
;
- при ![]()
![]() ;
;
- через эти точки
проводим прямую. При других частотах ![]() равна
равна ![]()
![]()
![]() .
.
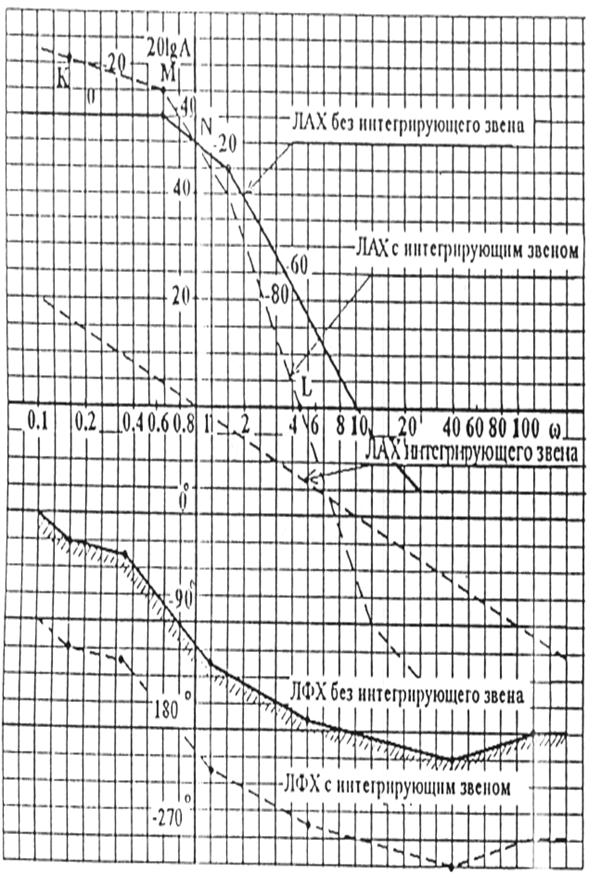
Рисунок 3.4 - Построение асимптотической ЛАХ и ЛФХ с интегрирующим звеном
Примечание
- При принятых допущениях фактически построена ЛФХ при ![]() т.е. для двойного апериодического звена.
При
т.е. для двойного апериодического звена.
При ![]() ЛФХ будет проходить
через значение -90° с большим наклоном. Но при асимптотическом способе
построения это пренебрегается.
ЛФХ будет проходить
через значение -90° с большим наклоном. Но при асимптотическом способе
построения это пренебрегается.
Асимптотическое построение ЛФХ характеристики форсирующего звена проводится аналогично, только угол будет положителен.
- при ![]()
![]() ;
;
- при ![]()
![]() ;
;
- при ![]()
![]() ;
;
ЛФХ
дифференцирующего звена равна ![]() , интегрирующего звена
, интегрирующего звена ![]() на всем диапазоне частот.
Построение логарифмической фазочастотной характеристики всей системы
производится путем геометрического сложения фазовой характеристики отдельных
звеньев. На рисунке 3,3показано построение ЛАЧХ без интегрирующего звена. На
рисунке 3,4 показано построение ЛАЧХ с интегрирующим звеном.
на всем диапазоне частот.
Построение логарифмической фазочастотной характеристики всей системы
производится путем геометрического сложения фазовой характеристики отдельных
звеньев. На рисунке 3,3показано построение ЛАЧХ без интегрирующего звена. На
рисунке 3,4 показано построение ЛАЧХ с интегрирующим звеном.
Определение устойчивости замкнутой СЛУ
Для определения устойчивости замкнутой СЛУ необходимо из точки, где ЛФХ принимает значение -1800 провести вертикальную линию до пересечения с ЛАХ. Если ЛАХ в этой точке имеет отрицательное значение (т.е. расположена ниже оси абсцисс), то замкнутая САУ устойчива. Если ЛАХ в этой точке имеет положительное значение (или расположена выше оси абсцисс), то замкнутая САУ неустойчива. Если ЛАХ в этой точке равна 0, то замкнутая САУ находится на границе устойчивости. При анализе устойчивости С АУ по критерию Найквиста по ЛАЧХ введено понятие:
ЗАПАС УСТОЙЧИВОСТИ ПО АМПЛИТУДЕ - это величина в децибелах, на которую надо увеличить коэффициент усиления, чтобы привести систему к границе устойчивости
![]()
где ![]() - частота при которой
- частота при которой ![]() ;
;
ЗАПАС УСТОЙЧИВОСТИ ПО ФАЗЕ – это угол, на который надо уменьшить фазочастотную характеристику, чтобы ее значение равнялось -1800.
![]() где
где ![]() - частота при которой
- частота при которой ![]() .
.
Определение запаса устойчивости по амплитуде и по фазе как показано на рисунке 3,7
ПРИМЕР 1 Определить запасы устойчивости замкнутой САУ, если ее структурная схема показана на рисунке 3,5 и передаточные функции звеньев равны
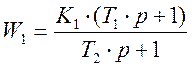
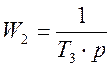
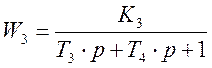
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
 |
Рисунок 3,5 – Структурная схема САУ к примеру 1
РЕШЕНИЕ
I Общая передаточная функция разомкнутой САУ (учитывая точку обрыва цепи) раина
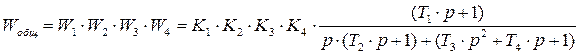
2 Построим систему координат в логарифмическом масштабе. Масштаб по оси абсцисс: 1 декада соответствует 5 см., по оси ординат: 20 децибел соответствует 2см. Ниже, через 2 см. проводим вторую ось абсцисс для фазовой логарифмической характеристики. Масштаб по оси абсцисс - тот же (1 декада - 5 см.) по оси ординат - 90 соответствует 2см. ( Рисунок 3.6)
3 Определяем собственную частоту каждого звена
Форсирующее
![]()
![]()
Апериодическое
![]()
![]()
Интегрирующее
![]()
![]()
Для определения собственной (резонансной) частоты колебательного звена представим в виде
![]()
тогда ![]()
Согласно полученным
значениям ![]() проводим
штриховые линии через ось абсцисс на рисунке 3,6
проводим
штриховые линии через ось абсцисс на рисунке 3,6
4 Вычисляем общий коэффициент усиления
![]()
![]()
5 ЛАЧХ построим в два этапа
1этап - без учета интегрирующего звена, (рисунок 3,6)
2этап - с учетом интегрирующего звена. (рисунок 3,7)
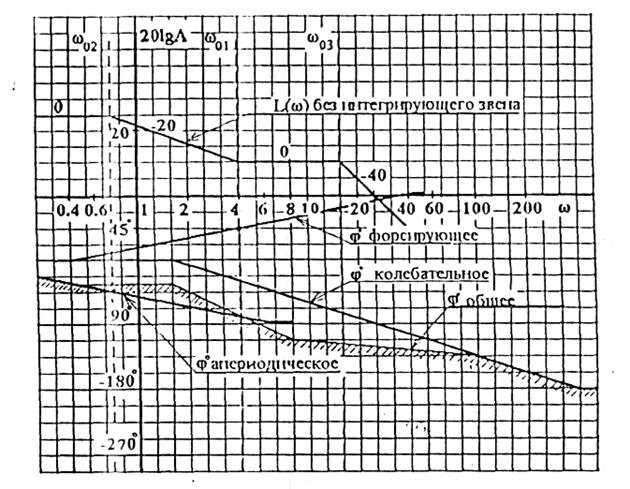 |
Рисунок 3.6 - Построение ЛАЧХ без учета интегрирующего звена (1этап)
6 Для построения фазочастотной характеристики по первому этапу определяем для апериодического звена
- при ![]()
![]() ;
;
- при ![]()
![]() ;
;
- при ![]()
![]() ;
;
для форсирующего звена
- при ![]()
![]() ;
;
- при ![]()
![]() ;
;
- при ![]()
![]() ;
;
для колебательного звена
- при ![]()
![]() ;
;
- при ![]()
![]() ;
;
- при ![]()
![]() ;
;
для интегрирующего звена ![]()
при любой частоте ( и первом этапе построения этот угол не учитывается)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.