Анализ линейной САУ.
По заданной структурной схеме системы управления вычислить эквивалентную передаточную функцию разомкнутой и замкнутой системы. Построить АФЧХ разомкнутой и замкнутой системы. Исследовать устойчивость по одному из критериев. Определить запасы устойчивости системы по амплитуде и по фазе. Построить переходный процесс системы методом трапеций, по переходному процессу провести анализ качества управления и определить все его показатели. При необходимости дать рекомендации методов улучшения этих параметров.
|
||||
|
||||
![]()
![]()

 xвх xвых
xвх xвых
 |
|||
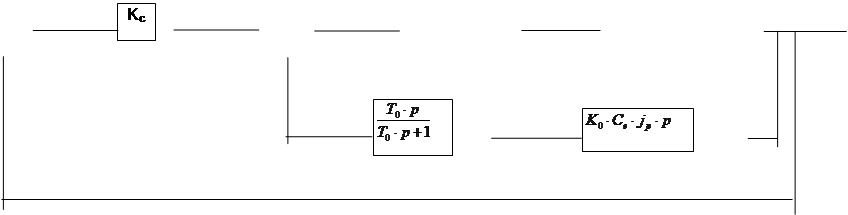
Рис. 1 – Структурная схема
Исходные данные:
|
Kс = 0.58; |
Td = 0.29; |
Ce = 0.033; |
|
KU = 0,48; |
Tm = 0.086; |
jp = 200. |
|
K0 = 184; |
T0 = 0.94; |
АФЧХ разомкнутой и замкнутой системы.
Вычислим эквивалентную передаточную функцию разомкнутой и замкнутой системы.
Обозначим передаточные функции звеньев:
![]()
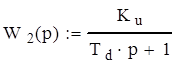
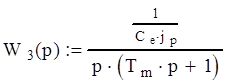
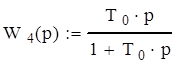
![]()
Вычислим передаточные функции для последовательного и параллельного соединения звеньев:
![]()
![]()
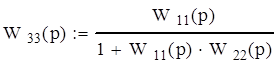
С учётом введённых обозначений передаточная функция разомкнутой системы имеет вид:
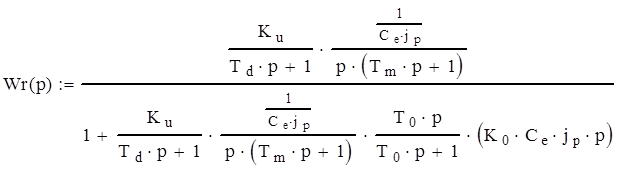
Упростим данное выражение
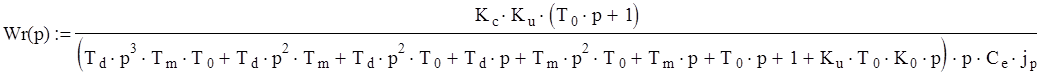
подставим значения коэфицентов в выражение для Wr(p):
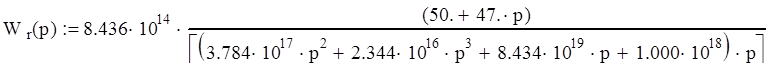
Построим АФЧХ, для этого заменим p = jw
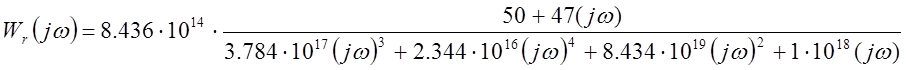
![]()
Преобразуем это выражение с учётом того, что ![]() :
:
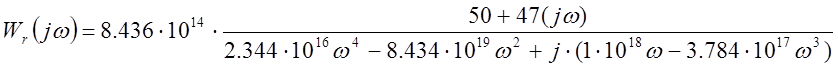
Выделим вещественную и мнимую часть
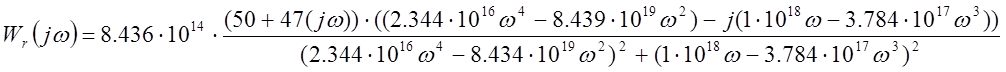 Выделим и упростим вещественную, мнимую части:
Выделим и упростим вещественную, мнимую части:
Wr(jω)=U(ω)+jV(ω)
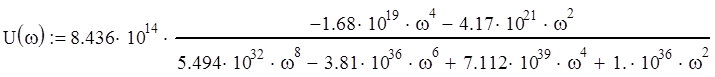
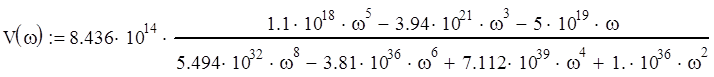
График АФЧХ разомкнутой системы представлен на рис.1, см. Приложение 1. На рис.2, приложения 1, представлен график АФЧХ разомкнутой системы в вблизи точки (0;j0).
Передаточная функция замкнутой системы имеет вид:
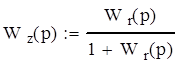
Упростим выражение и подставим значения коэфицентов:
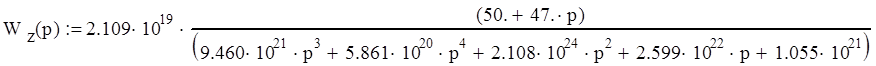
;
Построим АФЧХ, для этого заменим p = jw
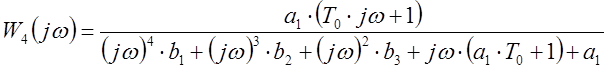 ;
;
Преобразуем выражение и выделим вещественную и мнимую часть
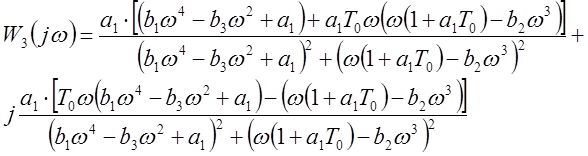
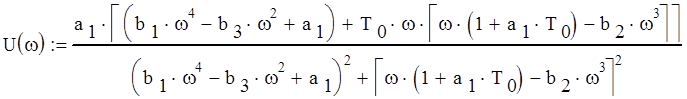
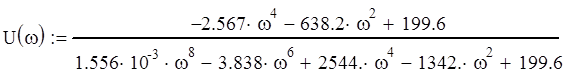
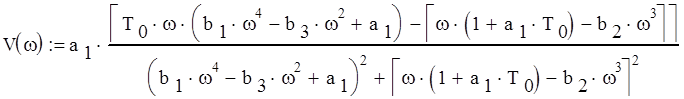
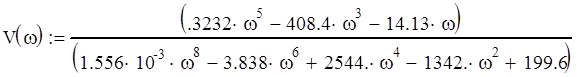
График АФЧХ замкнутой системы представлен на рис. 3, см. Приложение 1. На рис. 4, Приложения 1, представлен график АФЧХ в вблизи точки (0;j0).
Определение устойчивости системы.
Для определения устойчивости системы воспользуемся критерием Гурвица.
Критерий Гурвица: для того чтобы система управления была устойчива необходимо и достаточно, чтобы выполнялось неравенство а0 > 0, а все определители Гурвица были положительными.
Характеристическое уравнение имеет вид:
![]()
или
![]()
введем обозначение
с0 = b1;
c1 = b2;
c2 = b3;
c3 = a1T0+1;
c4 = a1.
Условие устойчивости с0 >0; с1 >0; с2 >0; с3 >0; с4 >0.
Определим определители Гурвица
c0 = 0.039 > 0;
c1 = 0.381 > 0;
c2 = 50.501 > 0;
c3 = 9.194 > 0;
c4 = 14.128 > 0;
![]()
![]() = 0.381
= 0.381
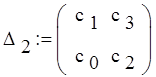
![]()
![]() = 18.888
= 18.888
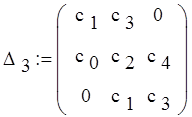
![]()
![]() = 171.616
= 171.616
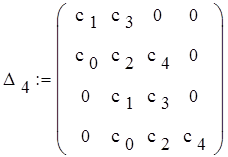
![]()
![]() = 2425
= 2425
Как видно из результатов, система по Гурвицу устойчива.
Используем графический метод Михайлова для определения устойчивости
Заменим p на jw в выражении D(p)
![]()
выделим реальную и мнимую часть
![]()
![]()
![]()
![]()
Система будет
устойчивой, если при возрастании частоты w от 0 до ¥
вектор D(jw) повернется на угол ![]() , где n – степень
уравнения D(p) = 0, или,
что то же самое, если характеристическая кривая при изменении частоты w от 0 до ¥, начиная с положительной действительной
оси, обходит последовательно в положительном направлении, т.е. против часовой
стрелки n квадрантов.
, где n – степень
уравнения D(p) = 0, или,
что то же самое, если характеристическая кривая при изменении частоты w от 0 до ¥, начиная с положительной действительной
оси, обходит последовательно в положительном направлении, т.е. против часовой
стрелки n квадрантов.
На рис. 2 приведена характеристическая кривая. Степень уравнения D(p) = 0 равна n = 4, как видно из рисунка характеристическая кривая последовательно проходит 4 квадранта и в 4 квадранте уходит в бесконечность, что соответствует устойчивой системе.
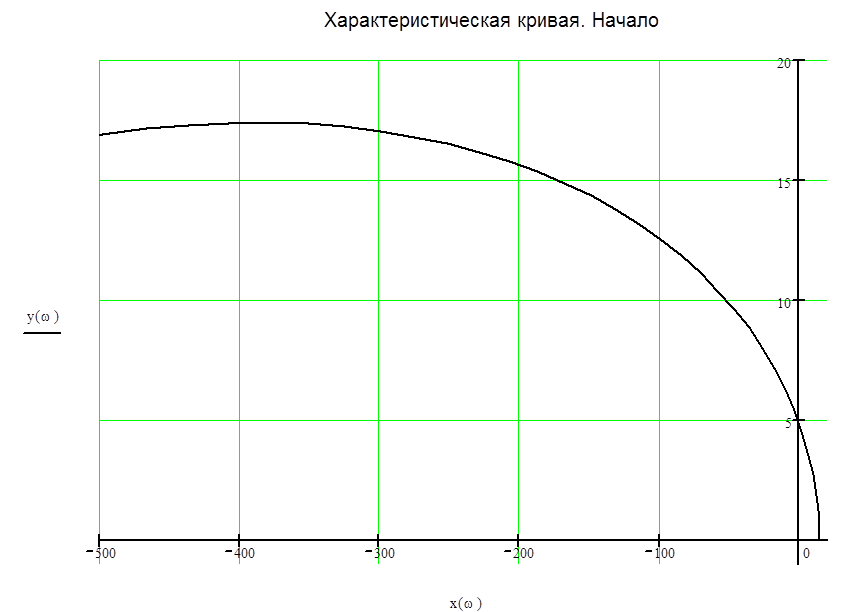
Рис. 2а – Характеристическая кривая. Область вблизи точки (0; j0)
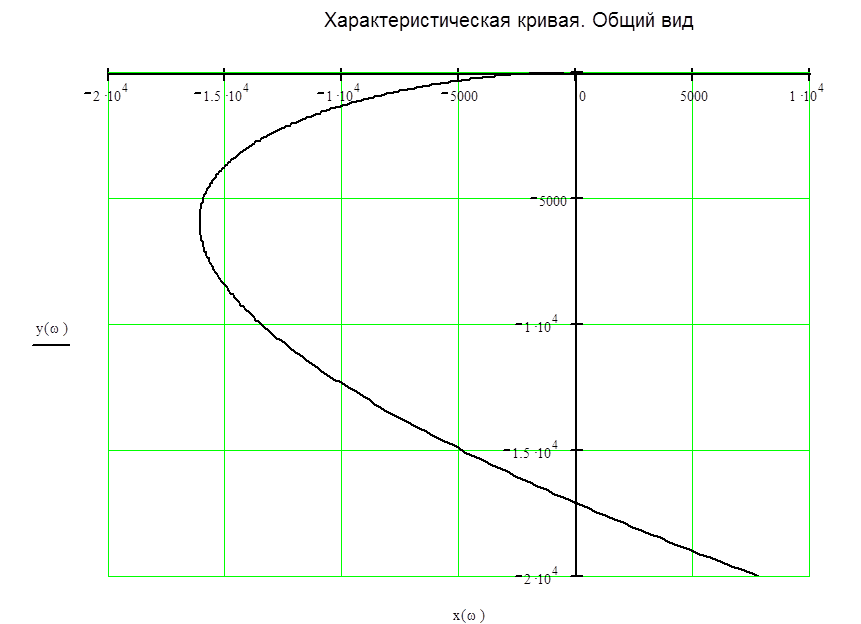
Рис. 2б.
Используя два критерия устойчивости, критерий Гурвица и критерий Михайлова, определили, что система является устойчивой.
Определение запаса устойчивости по амплитуде и по фазе.
Для этого построим ЛАХЧ и ФЧХ
![]() ;
;
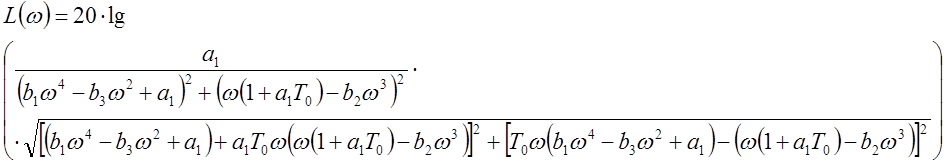
Подставим численные значения
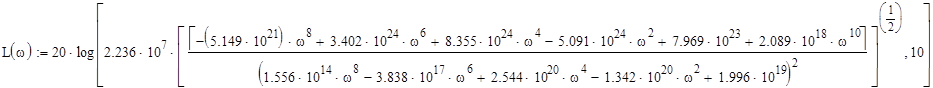
На рис. 5, Приложения 1, представлена ЛАЧХ характеристика.
ФЧХ определяется по следующей формуле
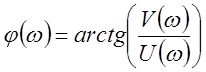 ;
;
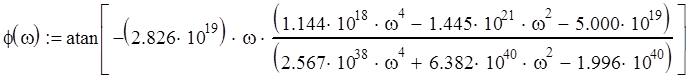
На рис. 6, Приложения 1, представлен график ФЧХ.
Из данного графика определим запасы устойчивости по амплитуде и по фазе
w = 0,7446 при данной частоте L(w) = 0;
Запас по фазе равен j = -48,868°
w = 35,551 при данной частоте j = -180°
Запас по амплитуде равен L(w) = 20 log (h) = -35.259 Þ h = 0.017
Переходный процесс.
Построим переходный процесс методом трапеции.
Для этого построим график вещественной частотной характеристики
![]()

|
|
|
|
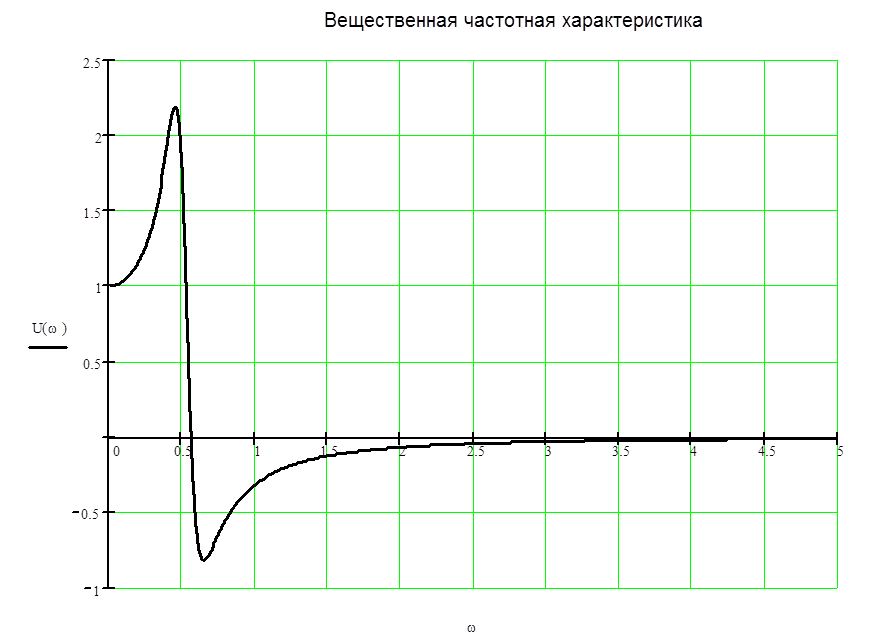
Рис. 3.
Разобьем вещественную частотную характеристику на трапециевидные частотные характеристики. Параметры трапеций занесем в таблицу.
Таблица №1
|
Трапеция |
Параметры трапеции |
|||
|
ro |
wd |
wn |
c |
|
|
1 |
-1,2 |
0,25 |
0,45 |
0,56 |
|
2 |
3 |
0,45 |
0,6 |
0,75 |
|
3 |
-0,6 |
0,65 |
1,1 |
0,59 |
|
4 |
-0,2 |
1,1 |
5 |
0,22 |
Значения составляющих кривой переходного процесса. Таблица №2
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.