Анализ систем автоматического управления по корневому методу: Методическое пособие к практическим работам

Международный Университет

      Бизнеса и Управления

                                                      БАЛАКОВСКИЙ

        ИНСТИТУТ

БИЗНЕСА И УПРАВЛЕНИЯ

ПРАКТИЧЕСКАЯ РАБОТА 

«АНАЛИЗ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ ПО КОРНЕВОМУ МЕТОДУ»

Методическое пособие к практическим работам  по курсу: «Теория автоматического управления»

для студентов специальностей 210100 – «Управление и информатика в технических системах»

230700 – «Сервис», 351400 – «Прикладная информатика»,

Одобрено

Редакционно-издательским

советом

Балаковского Института

Бизнеса и Управления

Балаково 2004

ЦЕЛЬ РАБОТЫ: научится анализировать САУ по значению полюсов и нулей передаточной функции.

ТЕОРИТИЧЕСКИЕ ПОЛОЖЕНИЯ

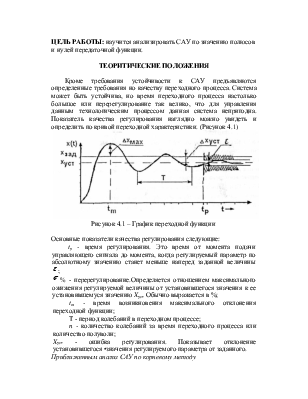
Кроме требования устойчивости к САУ предъявляются определенные требования но качеству переходного процесса. Система может быть устойчи­ва, но время переходного процесса настолько большое или перерегулирова­ние так велико, что для управления данным технологическим процессом данная система непригодна. Показатель качества регулирования наглядно можно увидеть и определить по кривой переходной характеристики. (Рисунок 4.1)

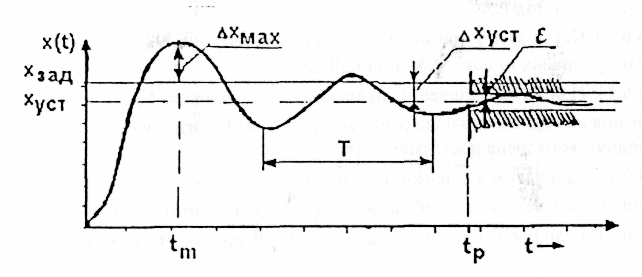
Рисунок 4.1 – График переходной функции

Основные показатели качества регулирования следующие:

t_p - время регулирования. Это время от момента подачи управляющего сигнала до момента, когда регулируемый параметр по абсолютному значе­нию станет меньше наперед заданной величины ;

% - перерегулирование.Определяется отношением максимального ожижения регулируемой величины от установившегося значения к ее уста­новившемуся значению X_уст Обычно выражается в %;

t_m - время возникновения максимального отклонения переходной функции;

Т - период колебаний в переходном процессе;

п - количество колебаний за время переходного процесса или количе­ство полуволн;

X_уст - ошибка регулирования. Показывает отклонение установившегося •значения регулируемого параметра от заданного.

Приближенным анализ САУ по корневому методу

Наиболее точно и наглядно эти показатели качества определяются пу­тем тем решения дифференциального уравнения и построения по нему графика переходной характеристики (рисунок 4.1). Это, так называемый, прямой ме­тод анализа. По этот метод трудоемкий, если дифференциальное уравнение высокого порядка (обычно, если n>4). Полос просто и без громоздких вычис­лений основные показатели качества САУ приближенно можно определить без нахождения уравнения переходной функции, по корневому методу, т. е. по взаимному расположению полюсов и нулей передаточной функции ( ПФ ) на плоскости корней (рисунок 4.3). Полюс ПФ определяется через корень характеристического полинома. Нуль определяется путем приравнивания ПФ к нулю или как корень полинома в числителе ПФ.

Основные показатели   качества САУ по корневому методу:

Степень устойчивости            (4.1)

где  - Расстояние от минимальной оси до ближайшего полюса системы (фактически оно равно минимальному значению корня). Поэтому показателю можно приближенно определить время регулирования:   

                                                                                        (4.2)

  Степень колебательности  

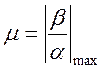                                                                                           (4.3)

           где    - минимальная часть корня характеристического полинома;

                    - вещественная часть этого корня

Поэтому можно определить перерегулирование

% =                                                                           (4.5)

ПРИМЕР 1 Определить степень устойчивости (), приближенное значение времени регулирования (t_p), степень коолебательности (), приближенное значение перерегулирования (%) по заданной ПФ сист:

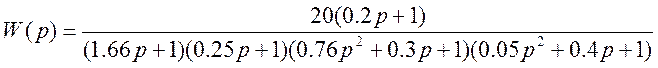
РЕШЕНИИЕ

1 Определяем корни характеристического уравнения

,   ,    ,  ,

2 Степень устойчивости                  (4.1) 

3 Приближенное значение времени перерегулирования                                                                              (4.2) 

4 Степень колебательности      (4.3)    

5 Приближенное значение перерегулирования

% =                                                         (4.4)

ОТВЕТ: Приближенное значение перерегулирования 

               Перерегулирование % =

Определение степени устойчивости без нахождения корней

Приближенное значение степени устойчивости можно определить и без нахождения корней характеристического полинома. Пусть дан характеристический полином устойчивой САУ.

определяем значение среднегеометрического корня.

 Задаемся предполагаемой степенью устойчивости , при условии <. Вводим новую переменную q=p+  или p=q- в характеристический полином (4.5). после алгебраических преобразований получаем  

В полученном полиноме все вещественные части корней уменьшили свое значение на величину предполагаемой степени устойчивости. Если корни но­вого характеристического полинома остались отрицательные (это можно проверить по любому критерию устойчивости), то данная СЛУ обладает сте­пенью устойчивости не менее

ПРИМЕР 1 Дан характеристический полином САУ 

                                        (4,7)

Определить обладает ли система степенью устойчивости равной  и определить время регулирования.

РЕШЕНИЕ

1 Определяем средний геометрический корень третьей степени

Заданная степень устойчивости  меньше среднегеометрического корня   , поэтому поставленная задача может иметь решение.

2  Вводим новую переменную q=p+1  или p=q-1  

3  Проверяем устойчивость полученного характеристического полинома по критерию Гурвица

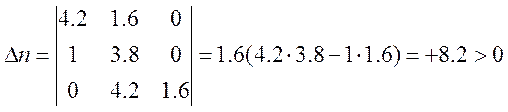
4  Определяем  приближенное значение времени регулирования

ОТВЕТ: полученный характеристический полином удовлетворяет критерию Гурвица, поэтому данная САУ обладает степенью устойчивости не менее единицы и имеет время регулирования не более 3 с.

ПРИМЕР 2 Проверим эту же систему на степень устойчивости

РЕШЕНИЕ

1 заданная степень устойчивости меньше среднегеометрического корня , поэтому поставленная задача может иметь решение.

2 Вводим новую переменную q=p+1.2  или p=q-1.2