Анализ систем автоматического управления по корневому методу: Методическое пособие к практическим работам, страница 2

3  Проверяем устойчивость полученного характеристического полинома по критерию Гурвица

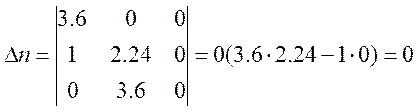
4  Определяем  приближенное значение времени регулирования

ОТВЕТ: , поэтому данная САУ обладает степенью устойчивости равной точно  и время        регулирования

Определение времени регулирования с учетом других полюсов и нулей

Для более точного определения времени регулирования надо учесть влияние других полюсов и нулей. Для этого выбирается доминирующий по­люс на плоскости корней и затем определяется влияние остальных полюсов и нулей на время регулирования по формуле [ 5, 7 ]

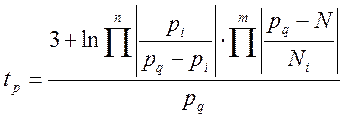                                                                                                                                                   (4.8)

где  - доминирующее значение полюса (принимается ближайший полюс к мнимой оси),

p – расположение полюсов,

 - расстояние между доминирующим полюсом и некоторым полюсом 

 - расстояние между доминирующим полюсом и некоторым нулем

ПРИМЕР 3 Определить время регулирования  по заданной ПФ

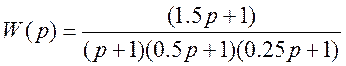
РЕШЕНИЕ

1 Определяем значения полюсов и нулей характеристического полинома

,   ,      

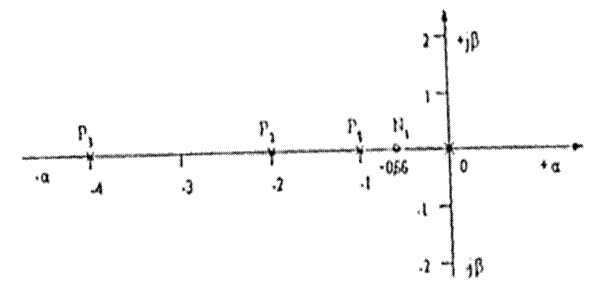
Покажем расположение полюсов на плоскости корней (рис. 4.2)

2 Определяем приближенное значение  по формуле (4.8)

   

                          Рисунок 4.2 – Расположение полюсов и нулей  на плоскости корней к  примеру 3

3 Определим более точное значение  по формуле (4.8)

в качестве доминирующего полюса P_q принимаем р₁=1 тогда;

         

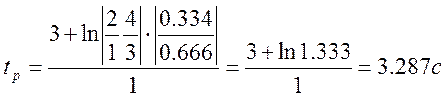
ОТВЕТ : время регулирования =3.287с.

Примечание  - Уравнение переходной функции по заданной ПФ следующее

Точное значение =3.14464 с. Ошибка вычисления корневым методом по формуле (4.8) в пределах 4.5% в сторону увеличения

ПРИМЕР 4 Определить время регулирования  по заданной ПФ

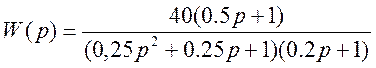
РЕШЕНИЕ

1 Определяем значения полюсов и нулей характеристического полинома

,   ,     

Покажем расположение полюсов на плоскости корней (рис. 4.3)

 

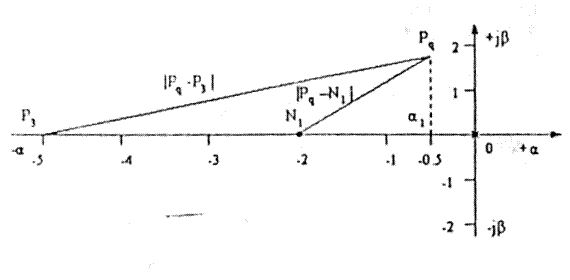Рисунок 4.2 – Расположение полюсов и нулей  на плоскости корней к  примеру 4

2 Степень устойчивости

3 Приближенное значение =3/0.5=6с

4 Определяем значение согласно расположению полюсов и нулей на плоскости корней по рисунку 4.3

в качестве доминирующего полюса принимаем  

Величину определяем из прямоугольника

Величину  определим из прямоугольника

5 По формуле (4.8) получаем

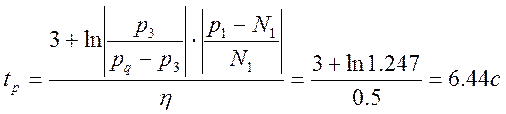
ОТВЕТ Время регулирования

Примечание

1 определить влияние полюса  на время регулирования. Для этого определим  по примеру 4 без учета полюса

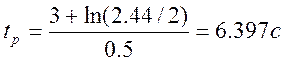
Ошибка расчета и пределах 0,7%. Поэтому, если ПФ имеет полюса, ко­торые удалены от доминирующего полюса на порядок (т. е. в 10 раз) и боль­ше, то при расчетеих влиянием можно пренебречь.

2 Определим влияние нуля n₁ = -2 на время регулирования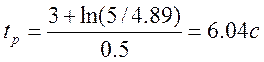

Ошибка в пределах 6 % поэтому такой полюс надо учитывать.

Определение основных показателей качества регулирования

а) Время наступления максимума производится по формуле (7)

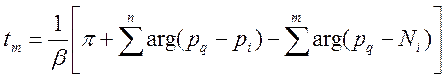            (4.9)

где  - Доминирующее значение полюса

        - минимальная часть комплексного доминирующего полюса,

        - расположение других полюсов на плоскости корней,

         - расположение нулей на плоскости

         arg – аргумент величины или  , т.е. угол в радианах относительно отрезка или  и осью абсцисс.

б) Величина максимального перерегулирования производится по формуле :

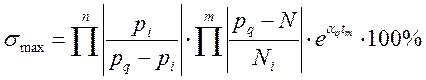                (4.10)

где  - вещественная часть доминирующего полюса,

        - время наступления первого максимума по формуле (4.9)

в) Количество колебаний за время переходного процесса:

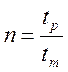                                                                                       (4.11)

где  - время регулирования

       - время наступления первого максимума,

г)  Период колебательного процесса переходной функции 

                                                                                      (4.12),

д) Определение ошибки регулирования в установившемся режиме

                                                                     (4.13)    

 где             - коэффициент статической ошибки

          Для статических систем коэффициент статической ошибки равен

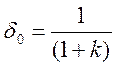                                                                             (4.14)

где  к – коэффициент усиления

   Для астатических систем коэффициент статической ошибки равен

                               (4.15)

ПРИМЕР 5 По данным примера 4 определить дополнительные показатели качества регулирования:

 - степень колебательности

 - время регулирования приближенное и точное

 - время первого максимума

% - перерегулирование

n – количество колебаний

  - коэффициент статической ошибки

РЕШЕНЕИЕ

1 Степень колебательности

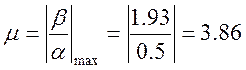
2 Приближенное значение перерегулирования:

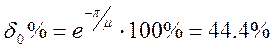
3 Для вычисления по формуле (4.9) вычислим  и

    

4 Определяем

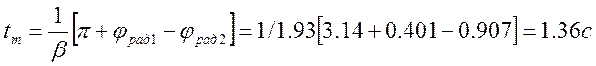
5 Значение  и определено в примере 4 и соответственно равно 5/4.89 и 2.44/2

6 Определяем   по формуле (4.10)

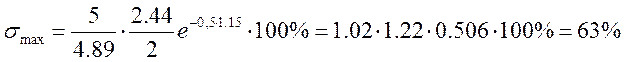
7 Определяем количество колебаний за  по формуле (4.11)

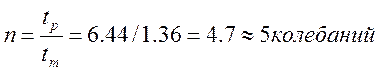
8 Определяем коэффициент статистической ошибки (4.12)

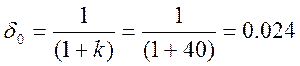
Результаты анализа САУ по примеру 4-5 приведены в таблице 4.1

Таблица 4.1 – Показатели качества САУ

			приближ	точно		% приближ	%  точно
-0.5j1.93	0.5	3.86	6.0	6.44	1.36	44.4	63	5

Примечание

1 Определение полюса на величину перерегулирования. Для этого определим % по примеру 5 без учета полюса

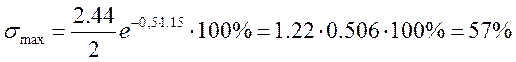
2 Определим влияние нуля  на величину перерегулирования

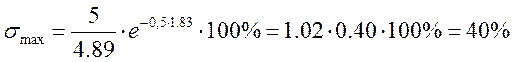
3 Определим величину перерегулирования, если не учитывать влияния полюса  и нуля

ВЫВОД: Приближенное значение перерегулирования определяется с учетом только доминирующего полюса. Остальные полюса уменьшают значение перерегулирования (в данном примере па 9,2%). Нули увеличи­вают значение перерегулирования ( в данном примере на 36,5%).

ИСХОДНЫЕ ДАННЫЕ

Задание 1

Провести анализ САУ  корневым методом  по заданной передаточной функции

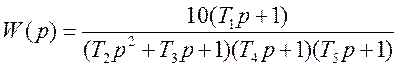
Параметры взять из таблицы 4.2

Таблица 4.2 – Параметры заданной ПФ