Анализ систем автоматического управления по интегральному критерию качества: Методическое пособие к практическим работам

Международный Университет

      Бизнеса и Управления

                                                      БАЛАКОВСКИЙ

        ИНСТИТУТ

БИЗНЕСА И УПРАВЛЕНИЯ

ПРАКТИЧЕСКАЯ РАБОТА 

«АНАЛИЗ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ ПО ИНТЕГРАЛЬНОМУ КРИТЕРИЮ КАЧЕСТВА»

Методическое пособие к практическим работам  по курсу: «Теория автоматического управления»

для студентов специальностей 210100 – «Управление и информатика в технических системах»

230700 – «Сервис», 351400 – «Прикладная информатика»,

Одобрено

Редакционно-издательским

советом

Балаковского Института

Бизнеса и Управления

Балаково 2004

ЦЕЛЬ РАБОТЫ: научиться вычислять квадратичную инте­гральную оценку качества процесса регулирования

ТЕОРИТИЧЕСКИЕ ПОЛОЖЕНИЯ

В основе анализа качества САУ по интегральному квадратичному кри­терию качества (ИКК) лежит интегральный показатель, характеризующий отклонение регулируемого параметра при переходном процессе от идеализи­рованного переходного процесса. В качестве идеального переходного про­цесса обычно принято считать ступенчатый переходный процесс, проте­кающий мгновенно, без перерегулирования. (Рисунок 5.1 а)

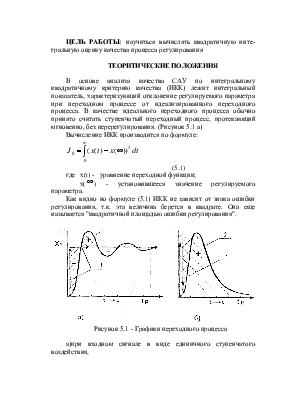
Вычисление ИКК производится по формуле:

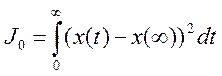                                                                                                                                      (5.1)

где   х(t) -   уравнение переходной функции;

        х() - установившееся значение регулируемого параметра.

Как видно но формуле (5.1) ИКК не зависит от знака ошибки регулиро­вания, т.к. эта величина берется в квадрате. Она еще называется "квадратич­ной площадью ошибки регулирования".

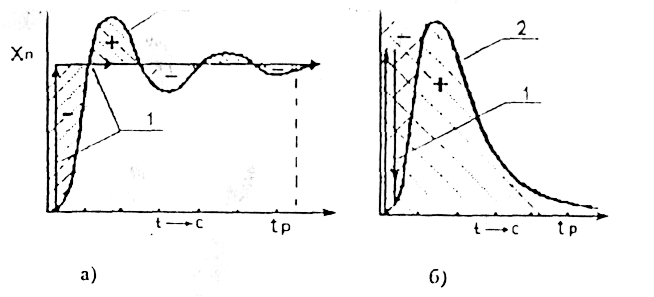
Рисунок 5.1 - Графики переходного процесса

а)при входном сигнале в виде единичного ступенчатого воздействия,

б)при входном сигнале в виде единичного импульса.

- идеализированный переходный процесс,

-  реальный переходный процесс.

Заштрихованная область показывает отклонение реальною переходно­го процесса от идеального;

знак (-) характеризует отставания реального переходного процесса от иде­ального;

знак (+) характеризует опережение  реального переходного  процесса по сравнению с идеальным.

Вычисление ИКК при ступенчатом входном сигнале

Пусть на вход САУ подан единичный, ступенчатый сигнал, тогда изобра­жение по Лапласу выходной координаты имеют вид:

                                                                                                                        (5.2)

Интеграл  можно вычислить, не производя обратного преобразования Лапласа, не решая дифференциального уравнения, не вычисляя затем интеграл (5.1), а сразу по коэффициентам формулы (5.2) [ 5, 7 ]

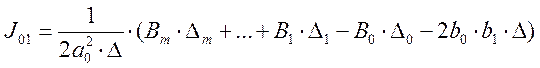                                                                                                   (5.3)

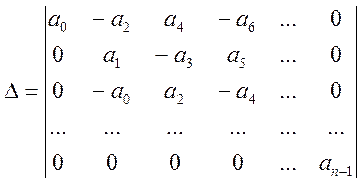
 определитель получаемый из путем замены i+1 столбца столбцом вида

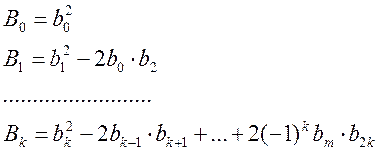
Таким образом, определение  проводится через раскрытие определите­ля Гурвица (д) и преобразованных определителей (,,...), что является трудоемким процессом. Поэтому для САУ пятого и выше порядка он практи­чески не применяется. Пусть для системы 4-го порядка изображение по Лап­ласу регулируемого параметра при скачкообразном входном воздействии име­ет вид:

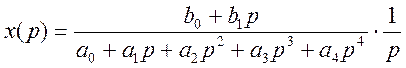                                                                                                                              (5.4)

Определяем значение  по формуле (5.3)

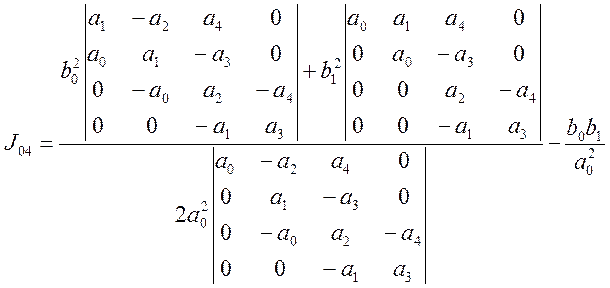                                                                                (5.5)

После раскрытия определителей формула (5.5) для системы 4-го порядка принимает вид:

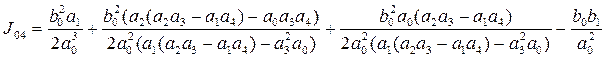                                                    (5.6)

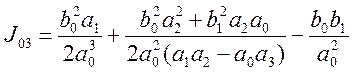                                                                                                                          (5.7)

Для системы 2-го порядка

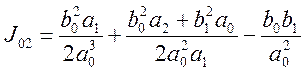                                                                                                                                    (5.8)      

Для системы 1-го порядка

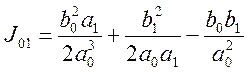                                                                                                                                                                  (5.9)

ПРИМЕР 1 Передаточная функция системы имеет вид:

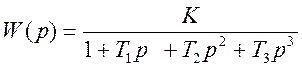
Определить оптимальное значение постоянной времени Т, соответст­вующую минимуму ИКК пли максимальному быстродействию системы при подаче на и ход системы ступенчатого сигнала И(t) = I(t) при следующих  па­раметрах К=10с^-1, Т, = 0.06с^-1, Т, = 0.04с¹.

РЕШЕНИЕ

1 Изображение по Лапласу выходной величины имеет вид: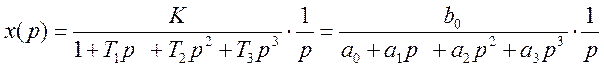                  

2 В соответствии с формулой (5.7) и  с учетом находим значение ИКК

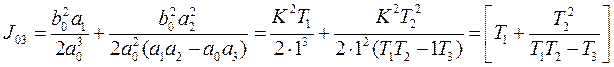
3 Для определения оптимального значения постоянной времени Т₁ соответствующего минимум ИКК, определим производную ИКК по Т, и приравняем ее нулю

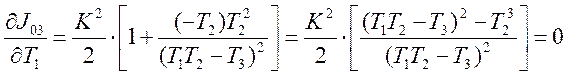
Из этого определяем значение Т₁

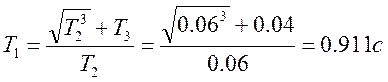
Примечание – проверим правильность полученного уравнения.  Для этого определим значение  при разных значениях Т_1.

ОТВЕТ: Оптимальное значение Т₁ по критерию минимум ИКК равно

Вычисления ИКК при импульсном входном сигнале

Пусть на вход системы подано возмущение в виде единичного импульса. Переходный процесс в виде импульсной переходной характеристики (весовая функция) показан па рисунке 5.16. Идеальный переходный процесс - это им­пульс с коэффициентом передачи К. Различие между идеальным и реальным переходным процессом показано в виде заштрихованной области и ее вели­чина может быть оценена через ИКК [5,7]. Изображение по Лапласу функции веса имеет вид

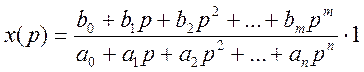                                                                                                                         (5.10)

ИКК весовой функции определяется по другой формуле [5,7]

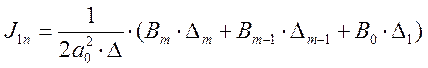                                                                                                            (5.11)

Значение ,,...    и  В₁  определяется также, как в формуле (5.3). Пусть изображение по Лапласу весовой функции имеет вид:

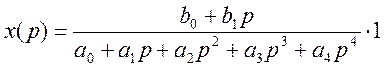
Определяем значение  по формуле (5.11)              

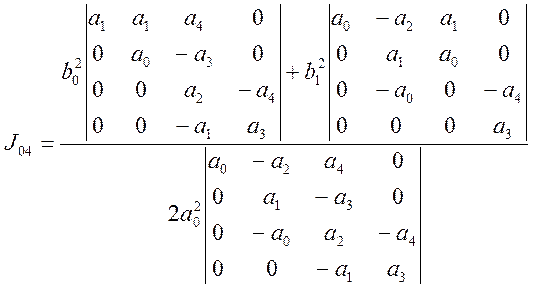                                                                                                     (5.12)