Анализ систем автоматического управления по интегральному критерию качества: Методическое пособие к практическим работам, страница 2

После раскрытия определителей формула (5.12) для системы 4-го порядка принимает вид:

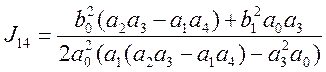                                                                                                                                              (5.13)

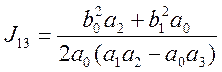                                                                                                                                                     (5.14)

Для системы 2-го порядка

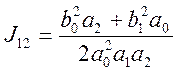                                                                                                                                                                            (5.15)    

Для системы 1-го порядка

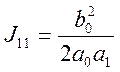                                                                                                                                                                                           (5.16)

ПРИМЕР 2 Передаточная функция системы имеет вид:

                   

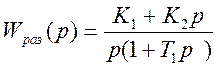
Определить оптимальное значение К₁ по критерию минимум ИКК при подаче на вход U(t)=I(t). Параметры системы К₁=20с¹, Т = 0.1с²

РЕШЕНИЕ

1 Передаточная функция замкнутой системы

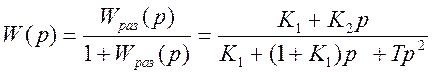
2 Изображение по Лапласу выходной величины

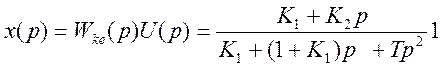
В соответствии с формулой (5.15) находим ИКК:

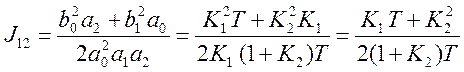
Для определения оптимального значения К₂ соответствующего минимум ИКК, определим производную ИКК по К₂ и приравняем ее нулю

 

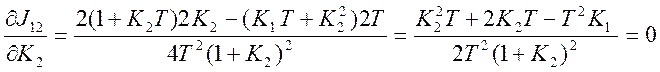
5 Из этого значения определяем значение К₂ при К₁=20с¹, Т = 0.1с²

      

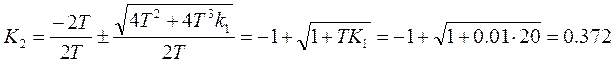
Примечание - проверим правильность полученного уравнения.  Для этого определим значение  при разных значениях К_2.

 

При
При
При

ОТВЕТ: Оптимальное значение К₂ по критерию минимум ИКК равно

Анализ САУ по улучшенному интегральному критерию качества

Недостаток ИКК в том, что при приближении действительной переход­ном функции к идеальной увеличивается колебательность и перерегулирова­ние, уменьшается запас устойчивости.

Поэтому широко применяется другая интегральная оценка, которая назы­вается улучшенным интегральным квадратичным критерием (УИКК). Он вычисляется по формуле:

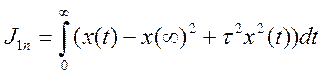                                                                                                                                               (5.17)

УИКК так же характеризует "квадратичную площадь ошибки регулиро­вания", по не относительно ступенчатом переходной функции, а определяется относительно экспоненциальной переходной функции с постоянной времени т (рисунок 5.2) и вычисляется УИКК по тем же формулам, как и ИКК.[5,7]

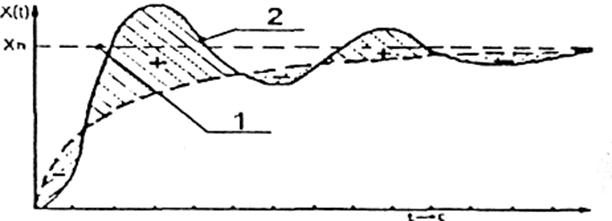
Рисунок 5.2 - Графики переходной функции

- идеальная переходная функция с ограничением по скорости возрастания

- реальная переходная функция;

заштрихованная область - отклонение реального переходного процесса от идеального.

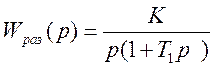
Определить оптимальное значение К по критерию  минимума  УИКК мри подаче на вход U(t)=I(t). Параметры системы T = 0,5с, ограничение по скоро­сти выходного сигнала равно т = 0,2с. РЕШЕНИЕ

1   Передаточная функция замкнутой системы:

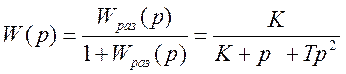
Изображение по Лапласу выходной величины  с учетом ограничения скорости т²

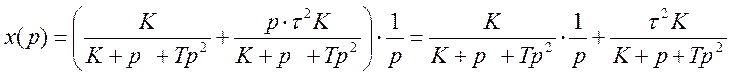
3 Как видно из полученного изображения регулируемой величины значе­ния УИКК можно представить как сумму двух ИКК. Первый ИКК определя­ется по формуле (5.8) при b₁= 0.

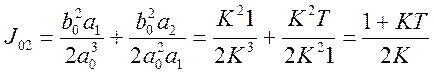
Второй ИКК определяется по формуле (5,15) при b₁= 0:

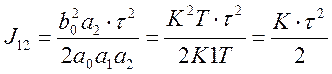
Результирующее значение УИКК:

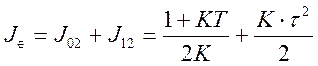
Для нахождения оптимального значения К определим производную УИКК по К и приравняем ее к 0.

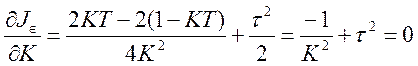
из этого уравнения определяем значение К: по УИКК К=5с^-1

Вычисление ИКК по ПФ ошибки регулирования

В некоторых случаях нахождение оптимального параметра по критерии минимума ИКК или минимума УИКК по изображению выходкой координаты по формуле (5.2) или (5.10) бывает достаточно сложным. Тогда ИКК или УИКК вычисляется по переходной составляющей ошибки регулирования.

Если дана передаточная  функция замкнутой САУ, то изображение пере­ходной составляющем ошибки регулирования определяется, но формуле:

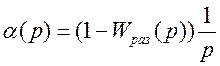                                                                                                                                                     (5.18)

Если дана передаточная функция разомкнутой САУ, то изображение пе­реходной составляющей ошибки регулирования определяется но формуле:

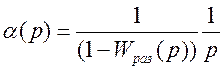                                                                                                                                                     (5.19)

Покажем определение ИКК по а(р) из конкретных примерах. [ 7 ]

ПРИМЕР 4  Передаточная функция замкнутой САУ имеет Вид

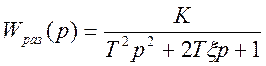
Определить оптимальное значение коэффициента затухания  по крите­рию минимума ИКК при входном сигнала U(t) =I (t).

РЕШЕНИЕ I Определяем ИKK но изображению регулируемой величины  х(р)

 1  Изображение регулируемой величины при входном сигнале U(t) =I (t).

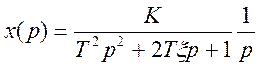
2 В соответствии с формулой (5.8) находим ИКК

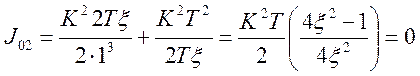
3 Определим производную ИКК по и приравниваем ее к 0

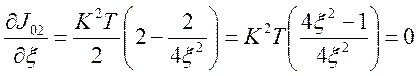
Из этого определяем значение

=0           

ОТВЕТ: Оптимальное значение =0,5

РЕШЕНИЕ 2   Определяем   ИКК по переходной составляющей ошибки регу­лирования   а(р)

1 Как видно из решения 1 значение коэффициента усиления К на нахожде­ние оптимального значение  влияния не оказывает. Поэтому для упрощения расчета принимаем К = 1.

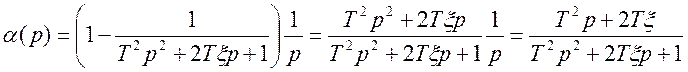
3 В соответствии с формулой (5.15) находим ИКК:

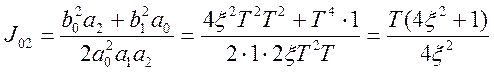
4 Определяем производную ИКК по  и приравнивая ее к 0

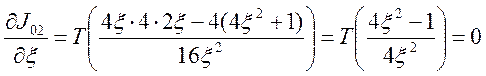
Из этого уравнения  определяем  

=0           

ОТВЕТ: Оптимальное значение по ИКК, полученное двумя способами, полностью совпадает и равно  =0,5

ПРИМЕР 5 Передаточная функция разомкнутой системы имеет вид 

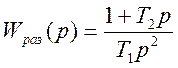
Определить оптимальное значение Т₁ по критерию минимума ИКК при подачи на вход U(t) =I (t). Определение оптимального значение Т₁, провести двумя способами.

РЕШЕНИЕ    а) по изображению регулируемой величины х(р)

Передаточная функция замкнутой системы:

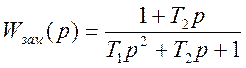
2  Изображение регулируемой величины

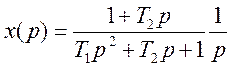
3  Значение ИКК по формуле (5.8)

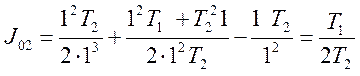
4 Очевидно что при

РЕШЕНИЕ: 6) по изображению составляющей ошибки регулирования а(р)

I   Изображение переходной составляющей ошибки регулирования по фор­муле (5.18)

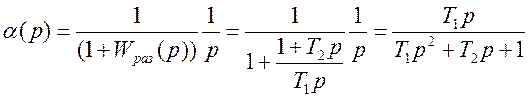
2  Значение ИКК по формуле (5.15)

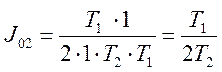
3 Очевидно что при

ОТВЕТ: Оптимальное знамение Т1 полученное через х(р) и а(р) , полностью совпадает и равно Т1 —> 0.