Теория параллельных прямых. Теория треугольника, страница 20

Теорема 4.3. В треугольнике: 1) против большей стороны лежит больший угол; 2) обратно, против большего угла лежит большая сторона.

Проверьте, будет ли верна эта теорема для вырожденных треугольников.

Отметим, что угол, лежащий против стороны, называют углом противолежащим этой стороне. А сторону, лежащую против угла, называют противолежащей этому углу.

Таким образом, теорема 4.3 дает возможность перенести отношение сторон на отношение противолежащих углов, а отношение углов на отношение противолежащих сторон.

Следствие 1. В прямоугольном треугольнике гипотенуза больше катета.

В самом деле, гипотенуза лежит против прямого угла, а катет – против острого. Так как прямой угол больше острого, то гипотенуза больше катета.

Следствие 2. Если два угла треугольника равны, то треугольник равнобедренный (признак равнобедренного треугольника).

Докажем этот признак. Пусть в треугольнике два угла равны. Тогда равны и стороны, лежащие против этих углов. Действительно, если предположить, что одна из указанных сторон больше другой, то угол, лежащий против нее, будет больше угла, лежащего против другой стороны, а это противоречит условию. Итак, в треугольнике две стороны равны, то есть он равнобедренный.

4.2.3. Соотношение сторон в треугольнике.

Осталось выяснить, произвольны ли длины сторон.

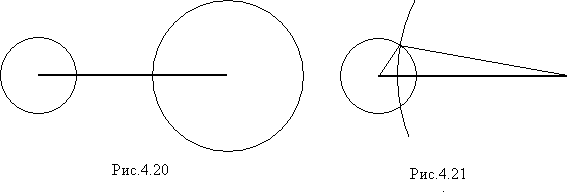
Возьмем произвольно три величины: 1см, 2см и 5см. И попробуем построить треугольник с такими длинами сторон. Отложим отрезок длиной 5 см, его концы окажутся двумя вершинами треугольника. Третью вершину будем искать с помощью циркуля (рис.4.20). Но окружности не пересекутся, а, значит, треугольник с такими длинами сторон не существует.

Треугольник получится, если взять длины 5см, 1 см и 4,5 см (рис.4.21). Видно, что для того, чтобы окружности пересеклись в двух точках, сумма их радиусов должна быть больше, чем расстояние между их центрами. Если сумма радиусов равна расстоянию между центрами, то мы получим вырожденный треугольник.

То есть в любом невырожденном треугольнике сумма длин двух любых сторон меньше длины третьей. Докажем это предположение.

Рассмотрим произвольный треугольник АВС и докажем, что АВ<АС+СВ.

Отложим на продолжении стороны АС отрезок СЕ, равный стороне СВ (рис.4.22). В равнобедренном треугольнике BCЕ Ð1=Ð2, а в треугольнике ABЕ ÐАВЕ>Ð1 и, значит, ÐАВЕ>Ð2. Так как в треугольнике против большего угла лежит большая сторона, то АВ<АЕ. Но АЕ=АС+СЕ=АС+СВ, поэтому АВ<АС+СВ. Таким образом мы доказали следующую теорему.

Теорема 4.4. Каждая сторона невырожденного треугольника меньше суммы двух других сторон.

Следствие. Для любых трех точек А, В и С, не лежащих на одной прямой, справедливы неравенства: АВ<АС+СВ, АС<АВ+ВС, ВС<ВА+АС. Каждое из этих неравенств называется неравенством треугольника.

4.3. Определение равенства треугольников.

Как вы помните, мы дали определение треугольника как представителя целого класса треугольников.

Иногда бывает важно конкретное местоположение треугольника. Как нам относиться к треугольникам, отличающимся только местоположением? Естественно назвать их равными. Напомним, что похожая ситуация у нас была с отрезками (как системой из трех элементов). Когда для нас стало важно конкретное расположение отрезков, мы ввели определение равных отрезков, как отрезков, может быть имеющих разные концы, но одинаковые длины.

Для треугольника, как системы из девяти элементов тоже можно попробовать дать определение равенства, отвлекаясь от конкретного местоположения вершин.

Однако точное определение равенства треугольников сталкивается с некоторыми трудностями. Дадим пробное определение.