Теория параллельных прямых. Теория треугольника, страница 16

Верно и обратное утверждение.

Лемма 3. Если параллельные прямые равноудалены, то отрезки секущей, расположенной между параллельными прямыми равны.

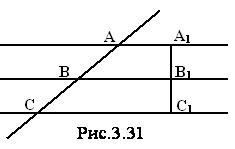
Доказательство. Нам дано, что A₁В₁=B₁C₁ и A₁C₁^CC₁(рис.3.31). Докажем, что АВ=ВС.

Через точку В проведём прямую DE, параллельнуюA₁C₁ (рис. 3.32, а). Так как прямые AA₁, BB₁, CC₁ параллельны и прямая DE параллельна прямой A₁C₁,тоDB=A₁B₁ иBE=B₁C₁, и значит DB=BE (по лемме 1).

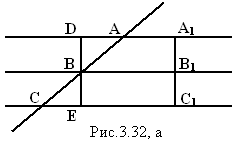УглыÐCBE и ÐABD равны как вертикальные и равны отрезки DB и BE. Углы ÐАDB и ÐСЕB равны как внутренние накрест лежащие при параллельных прямых  AA₁ иCC₁ и  секущейDE.

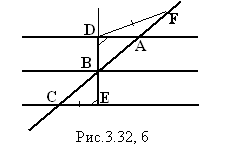На луче BА отложим отрезок BF, равный отрезку BС (рис.3.32, б). Углы ÐCBE и ÐDBF равны, значит, их соответственные поперечины CE и DF равны (проверьте, действительно ли они являются соответственными). То есть BF и BC – соответственные поперечины углов ÐFDB и ÐECB, но они равны по построению, а значит, угол ÐFDB равен углу ÐECB. Но угол ÐECB равен углу ÐADB. Это означает, что равны углы ÐFDB иÐADB, то есть точка F лежит на луче AD. По построению точка F лежит на луче ВA. Но эти лучи пересекаются в точке A, то есть точки A и F совпадают и AB=BF=BC. Следовательно, BA=BC. Утверждение леммы 3 доказано.

Если мы обобщим наши рассуждения, то сможем сформулировать теорему для большего количества прямых.

3.5. Взаимное расположение пяти прямых.

Задание 5. На рисунке 3.31 изображены три случая взаимного расположения прямых. Каждый из них обобщает какую-нибудь лемму. Подумайте, какую именно. Изобразите остальные случаи взаимного расположения пяти прямых.

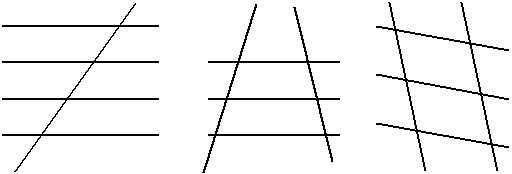
Рис.3.33

Теорема 3.6 (теорема Фалеса). Если три параллельные прямые, пересекающие две данные прямые, отсекают на одной прямой равные между собой отрезки, то они отсекают равные между собой отрезки и на другой прямой.

Доказательство. Пусть А₁,А₂,А₃ - точкипересечения параллельных прямых с одной из данных прямых и А₂ лежит между А₁ и А₃. И пусть В₁, В₂ ,В₃ - соответствующие точки пересечения этих прямых с другой прямой (рис.3.34). Докажем, что если А₁А₂=А₂А₃, то В₁В₂=В₂В₃.

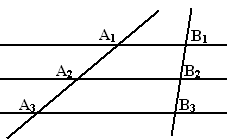
Рис.3.34

Так как А₁А₂=А₂А₃, топо лемме 2 расстояние между прямыми А₁В₁, А₂В₂, равнорасстоянию между прямыми А₂В₂, А₃В₃, тогда по лемме 3 В₁В₂=В₂В₃. Теорема доказана для трех параллельных прямых.

Замечание. Равные отрезки можно откладывать от точки пересечения секущих, то есть так: АВ₁=В₁В₂=В₂В₃. Тогда и на другой прямой равные отрезки надо считать от точки пересечения, т.е. так: АА₁=А₁А₂=А₂А₃.