Теория параллельных прямых. Теория треугольника, страница 12

На рисунке 3.17, а видно, что углы 1 и 2 равны, а также равны углы 3 и 4 на рисунке 3.17, б.

Заметим, что, если продолжить прямые на рисунках 3.16, а, б, то они пересекутся в некоторой точке. Прямые на рисунках 3.17, а, б параллельны. Получается, что параллельность прямых и равенство внутренних накрест лежащих углов связаны. Возможно, имеют место какие-то из этих утверждений:

Ø  Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.

Ø  Если две параллельные прямые пересечены секущей, то внутренние накрест лежащие углы равны.

Первое утверждение отвечает на вопрос 1 и является признаком параллельности прямых.

Сформулируйте соответствующие утверждения для не параллельных прямых.

Признаки параллельности.

Теорема 3.1(I признак параллельности двух прямых). Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.

Доказательство. Пусть прямые a и b образуют с секущей AB равные внутренние накрест лежащие углы. Допустим, прямые a и b не параллельны, а значит, пересекаются в некоторой точке C (рис.3.18). Секущая AB разбивает плоскость на две полуплоскости. В одной из них лежит точка C.

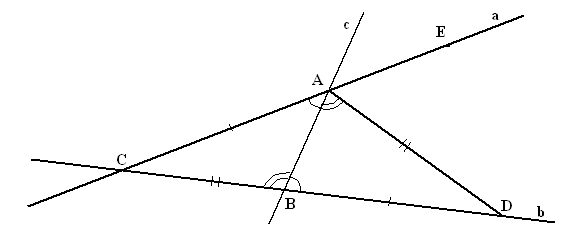
Рис.3.18

Отложим на прямой b отрезок BD,равный отрезку AC так, чтобы точки C и D лежали в разных полуплоскостях. Проведем поперечину AD угла ABD.Углы ÐCAB и ÐABD равны по условию (как внутренние накрест лежащие углы при прямых a и b и их секущей AB). Значит равны их соответствующие поперечины AD и BC.

Углы ABC и BAD равны, так как равны их соответствующие поперечины AC и BD. Углы ABC и BAE равны по условию. Следовательно, углы BAD и BAE равны, кроме того, они совпадают (так как у них сторона AB общая, и они лежат в одной полуплоскости) и, значит, точка D лежит на прямой а.

Получается, что через точки C и D проходят две различные прямые a и b. А мы знаем, что через любые две точки можно провести единственную прямую. Мы получили противоречие. Значит, прямые a и b параллельны. Теорема доказана.

Следствие 3. Две прямые, перпендикулярные третьей, параллельны.

Задание 1. Попробуйте доказать это самостоятельно.

Теорема 3.2(обратная теореме 3.1). Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.

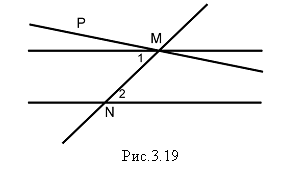Доказательство. Пусть параллельные прямые a и b пересечены секущей MN. Допустим, что накрест лежащие углы 1 и 2 не равны и Ð2 больше Ð1. Отложим от луча MN угол PMN, равный углу 2, так, чтобы угол PMN и угол 2 были накрест лежащими углами при пересечении прямых MP и b секущей MN (рис.3.19).

По построению эти накрест лежащие углы равны, и, значит, по теореме 3.1 MPúúb. Мы получили, что через точку M проходят две прямые (прямая a и прямая MP), параллельные прямой b. Но это противоречит аксиоме параллельности. Значит, наше допущение неверно и угол 1 равен углу 2. Теорема доказана.

Сформулируйте обратную теорему к теореме 3.2.

Следствие 4. Если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна и другой.

Задание 2. Докажите это следствие и сформулируйте обратное.

Вернемся к углам с вершинами в точках пересечения прямых и секущей, так как мы рассмотрели не все характеристические пары.

На рисунках 3.20 и 3.21 можно увидеть две пары внутренних накрест лежащих углов. Но эти же углы входят в состав других пар: 1 и 2, а также 3 и 4.