Теория параллельных прямых. Теория треугольника, страница 14

Если при пересечении двух прямых секущей сумма внутренних односторонних углов не равна 180°, то прямые не параллельны, то есть при достаточном продолжении пересекаются.

Доказательство. Если бы эти прямые не пересекались, то они были бы параллельны, и тогда сумма внутренних односторонних углов равнялась бы 180°, что противоречит условию. Теорема доказана.

Сформулируйте обратную теорему.

3.3. Взаимное расположение четырех прямых.

Мы изучили различные случаи взаимного расположения двух и трёх прямых на плоскости. Теперь изучим взаимное расположения четырёх прямых на плоскости. Изобразим разные случаи.

а) две пересекающиеся прямые пересекают две другие пересекающиеся прямые:

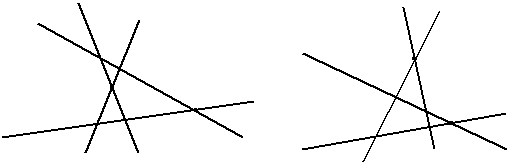
Рис.3.22

б) каждая из двух пересекающиеся прямых пересекает две параллельные прямые:

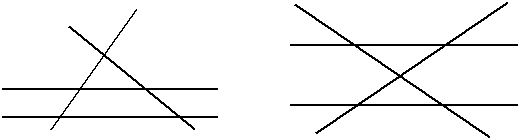
Рис.3.23

в) две параллельные прямые пересечены двумя параллельными прямыми:

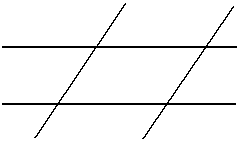
Рис.3.23

г) три параллельные прямые пересечены третьей прямой:

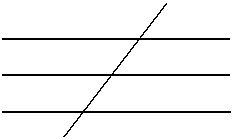
Рис.3.24

д) все четыре прямые параллельны:

Рис.3.25

Какие фигуры вы можете увидеть на этих рисунках? Например, на рис.3.23, слева, видна фигура, состоящая из четырех отрезков, два из которых параллельны. На рис.3.23 видно, что при пересечении двух параллельных прямых двумя другими параллельными прямыми получилась фигура, у которой противоположные стороны попарно параллельны и равны. Докажем это.

Лемма 1. При пересечении двух параллельных прямых двумя другими параллельными между собой прямыми получается фигура, у которой противоположные стороны параллельны.

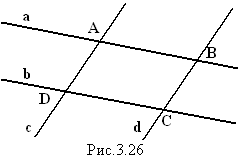Доказательство. Пусть параллельные между собой прямые a, b и параллельные между собой прямые c, d пересекаются в точках A, B, C, D (рис.3.26).

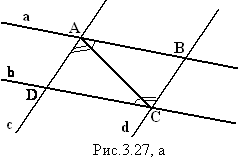Докажем, что АВ=СD и АD=ВС. Проведём отрезок АС (рис.3.27, а). Для начала докажем, что АВ=СD.

Углы ÐACD иÐСAB равны как внутренние накрест лежащие при параллельных прямых a и b и секущей AC. Углы ÐDAC иÐACB равны как внутренние накрест лежащие при параллельных прямых c и d и секущей AC.

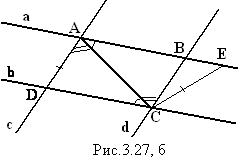На луче АВ отложим отрезок АЕ, равный отрезку CD (рис.3.27, б). Углы ÐACD иÐСAE равны, значит, их соответственные поперечины AD и CE равны. То есть АЕ и DC – соответственные поперечины углов ÐDAC иÐACB, но они равны по построению, а значит, угол ÐACЕ равен углу ÐDAC. Но угол ÐDAC равен углу ÐACB. Это означает, что равны углы ÐACЕ иÐACB, то есть точка Е лежит на луче СВ. По построению точка Е лежит на луче АВ. Но эти лучи пересекаются в точке В, то есть точки В и Е совпадают и АВ=АЕ=CD.

Итак мы доказали, что равны отрезки АВ и СD. Отрезки AD и CB равны как  соответственные  поперечины  равных углов.  Утверждение  леммы 1  доказано.

Следствие 5: Противоположные углы фигуры ABCD равны (рис.3.27).