Пробное учебное пособие по темам «Ломаная», «Четырехугольник», «Площадь» для восьмого класса, страница 23

Были выделены следующие возможные варианты подходов:

1)  Классические четырехугольники решают проблему фигуры, получающейся при пересечении двух параллельных прямых двумя другими параллельными прямыми.

2)  Классические четырехугольники решают проблему особенных случаев четырехугольника.

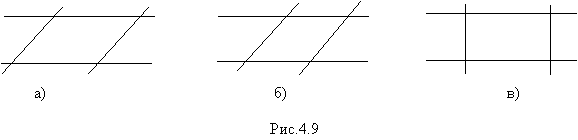
Работая в первом подходе, параллелограмм получим при пересечении двух параллельных прямых двумя другими параллельными прямыми (рис.4.9.а). Ромб и прямоугольник получатся как особые случаи пересечения пар параллельных прямых: ромб получается при пересечении двух параллельных прямых двумя другими параллельными прямыми, находящимися друг от друга на том же расстоянии, что и первые две (рис.4.9.б); прямоугольник получается, когда пары параллельных прямых взаимно перпендикулярны (рис.4.9.в). При объединении обоих особых случаев пересечения пар параллельных прямых получается квадрат.

Трапецию через соотношения четырех прямых получить нельзя. (При пересечении двух параллельных прямых двумя другими прямыми возникает проблема фигуры, описанная в пункте 1).

Против первого подхода выступает способ получения многоугольника (соединение отрезков концами). Так как четырехугольники идут после многоугольников, то и задаваться они должны как многоугольники. Имея целью рассматривать четырехугольники как примеры исследования n-угольников, авторы не могли поместить главу «Четырехугольники» раньше главы «Ломаная».

Второй подход, который мы назвали формально-классификационным, также имеет свои недостатки.

Особенные случаи фигуры получаются, когда на ее элементы накладываются некоторые условия (ограничения).

Для выделения особых случаев четырехугольника можно исходить из логики отношения сторон (накладывать ограничения только на стороны четырехугольника), из логики отношений углов или из логики смешанных отношений сторон и углов.

Если следовать логике отношения сторон, то получится очень громоздкая классификация четырехугольников. Накладывая ограничения только на две стороны, мы получим более пяти типов четырехугольников: четырехугольник с равными сторонами (соседними и противолежащими), четырехугольник с перпендикулярными сторонами (соседними и противолежащими), четырехугольник с параллельными сторонами, четырехугольник с равными параллельными сторонами, четырехугольник с равными перпендикулярными сторонами (соседними и противолежащими).

Не менее громоздкой классификация четырехугольников получится, если исходить из логики смешанных отношений сторон и углов.

Самой выгодной представляется логика отношения углов. Так как на углы можно наложить только условие равенства, то всего получится 6 типов четырехугольников: четырехугольник с двумя равными соседними углами (рис.4.10.а), четырехугольник с двумя равными противолежащими углами (рис.4.10.б), четырехугольник с тремя равными углами (рис.4.10.в), четырехугольник со всеми равными углами (рис.4.10.г), четырехугольник, у которого противолежащие углы попарно равны (рис.4.10.д) и четырехугольник, у которого соседние углы попарно равны (рис.4.10.е).

Ромб в логике отношения углов появится как особый случай параллелограмма, квадрат появится как особый случай прямоугольника.

Трапеция здесь может появиться только как особый случай произвольного четырехугольника, поэтому ее рассмотрение возможно лишь после остальных четырехугольников. Авторы же считают, что трапеция должна «открывать» изучение классических четырехугольников.

Действуя в формально-классификационном подходе в логике смешанных отношений, мы не стали рассматривать все возможные сочетания отношений, в которых могут находиться элементы четырехугольника. (Сделать это и рассмотреть свойства получившихся четырехугольников мы предлагаем на факультативных занятиях.) Чтобы не перегружать учебник, мы по отдельности рассмотрели каждое отношение на разном количестве элементов.