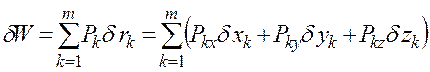Динамика жесткой машины с одной степенью подвижности, страница 2

.

Но так как                    ;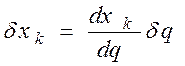

то                            .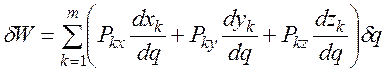

Следовательно, обобщенная сила, соответствующая всем силам сопротивления, составит

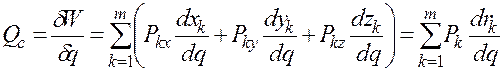.                                                                                                                   (2.10)

Если учесть, что

;  ;   ,

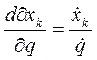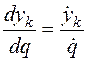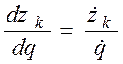то из (2.10) можно получить следующее выражение для обобщенной силы:

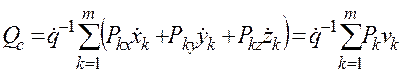                                                                                                                   (2.11)

Таким образом, мощность  равна, сумме мощностей, соответствующих всем активным силам сопротивления, действующим на движущиеся звенья механической системы машины.

Если обобщенная координата является линейной, то обобщенная сила имеет размерность силы; в этом случае ее называют приведенной силой сопротивления; если же обобщенная координата является угловой, то обобщенная сила имеет размерность момента и называется приведенныммоментом сил сопротивления. В дальнейшем для определенности будем предполагать последнее и обозначать обобщенную силу через М_с.

Силы полезного сопротивления обычно могут быть представлены как функции координат и скоростей точек их приложения. В аналогичном виде могут быть представлены и другие силы сопротивления. Таким образом, можно считать, что

,

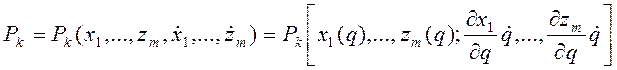т. е. что активные силы, а, следовательно, и их проекции на оси могут быть представлены как функции обобщенной координаты q и обобщенной скорости . Тогда из выражения (2.10) следует, что обобщенные силы сопротивления также могут быть представлены в виде функций q и:

.                                                                                                                   (2.12)

В дальнейшем будем предполагать, что приведенный момент сил сопротивления, действующих в машине, приводится к виду (2.12). В более общем случае он может зависеть также явно от времени t и от .

Предположим, что все силы сопротивления приложены к звеньям исполнительного механизма, а q – угол поворота выходного звена   двигателя. Тогда М_с(q, ) – периодическая функция q с периодом 2pi. Выделив из нее среднюю составляющую

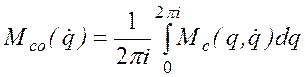,                                                                                                                   (2.13)

представим M_c в виде (см. рис. 2.7)

,                                                                                                                   (2.14)

где  — периодическая функция q, не содержащая постоянной составляющей.

Функция М_с0() определяет зависимость среднего значения приведенного момента сил сопротивления от угловой скорости выходного вала двигателя. В дальнейшем эту функцию  будем называть средним моментом сил сопротивления. Как правило, с увеличением скорости средний момент сил сопротивления возрастает и зависимость (2.13) имеет форму кривой 1 на рис. 2.3. Однако в некоторых случаях (на малых скоростях вращения) производная  отрицательна и зависимость (2.13) имеет форму, соответствующую кривой 2. Это уменьшение М_с0 () объясняется тем, что силы трения покоя существенно больше, чем силы трения скольжения, и при увеличении скорости машины на первых порах происходит уменьшение сил трения.

Мс0                   0                                        Рис. 2.3. Средний момент сил сопротивления

Силы сопротивления, действующие на звенья двигателя, будем добавлять к движущему моменту и предполагать, что в статической характеристике двигателя (1.6) учтено  влияние этих сил.

2.3. Уравнения движения машин. Режимы движения

Вывод уравнений движения. Составим уравнение движения механической системы с одной степенью свободы в виде уравнения Лагранжа второго рода

.

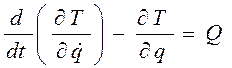Используя 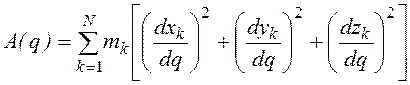 и предполагая, что q — угловая координата A(q) ºJ(q) — приведенный момент инерции машины, а также учитывая (2.12), находим

                                  .             

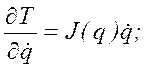
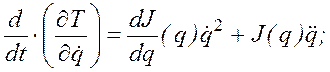
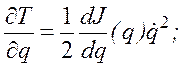
Отсюда получаем уравнение движения в виде

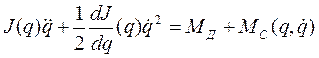                                                                                                                   (2.15)