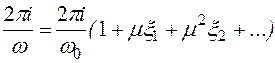Динамика жесткой машины с одной степенью подвижности, страница 15

,

где      - подлежащие определению постоянные.

Одновременно преобразуем независимую переменную t, введя
новую переменную :

.

Легко видеть, что при этом решение (2.64) преобразуется к виду

                                                                                                                   (2.66)

причем функции   по аргументу  имеют период .

В дальнейшем ограничимся отысканием второго приближения, т.е. учетом в (2.66) слагаемого порядка. Дифференцируя (2.66) по t и, сохраняя в полученных выражениях члены порядка , имеем:

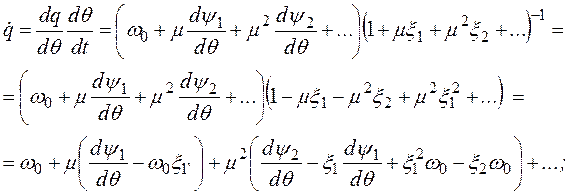                                                                                                                (2.67)

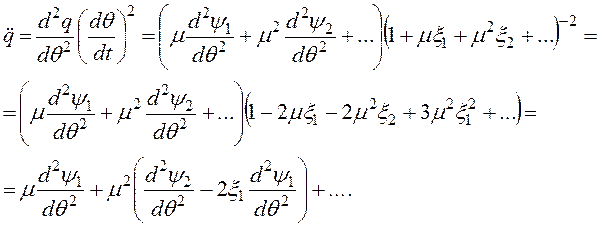                                                                                                                (2.68)

Для определения функций  и постоянных  подставим (2.67) и (2.68) в (2.63) и приравняем в левой и правой частях члены одинаковой степени относительно . При этом будем следить за тем, чтобы функции  не содержали членов, линейных относительно . Входящие в уравнение (2.63) нелинейные функции     разложим в степенные ряды, сохраняя столько членов, сколько необходимо для учета всех слагаемых, имеющих степень не выше второй относительно параметра . В результате получим

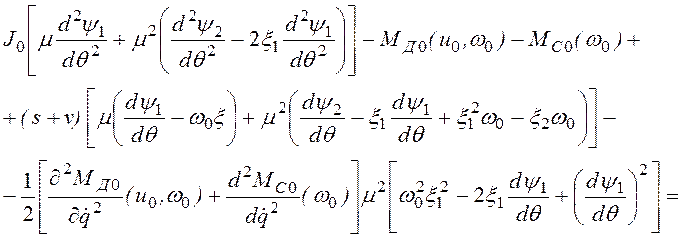
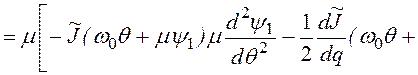                                             (2.69)

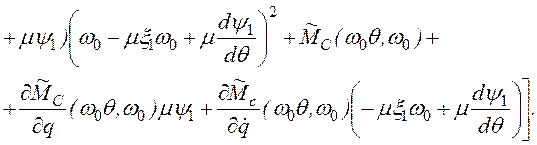
Приравнивая слева и справа члены, не содержащие , имеем

.

Из этого уравнения, совпадающего с ранее полученным уравнением (2.27), определяется значение , а, следовательно, и порождающее решение , совпадающее прис ранее полученным решением .

Приравнивая члены первой степени относительно, получаем

,

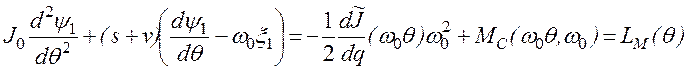или

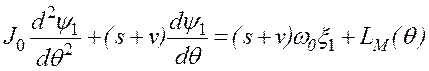.                                                                                                                (2.70)

Для того чтобы решение этого уравнения  не содержало слагаемого, линейного относительно , должно выполняться условие . Таким образом, уравнение первого приближения (2.70) тождественно совпадает с ранее полученным уравнением (2.43) (при ), поскольку при  имеем . Следовательно, полученное выше решение (2.45) при  является решением уравнения (2.63), найденным с точностью до членов первой степени относительно  и соответствующим значению .

Приравнивая теперь в (2.69) члены порядка  и учитывая, что , имеем

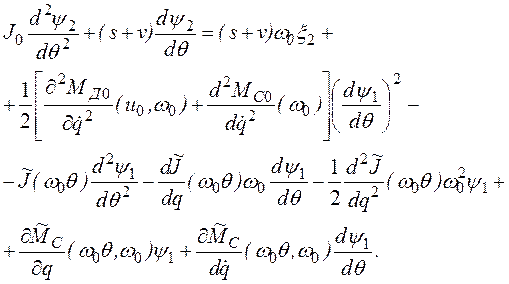                                                                                                                (2.71)

Поскольку функция  уже определена из уравнения первого приближения, уравнение (2.71) является линейным дифференциальным уравнением для неизвестной функции , правая часть которого представляет собой периодическую функцию с периодом . Для того чтобы в частном решении этого уравнения не появилось линейных относительно  слагаемых, постоянная составляющая правой части должна быть равна нулю. Отсюда получаем соотношение, позволяющее найти ₂:

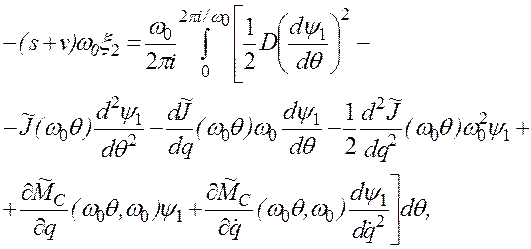                                                                                                                (2.72)

где                           .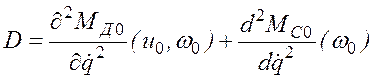

Упростим выражение, стоящее в правой части. Во-первых, учтем, что

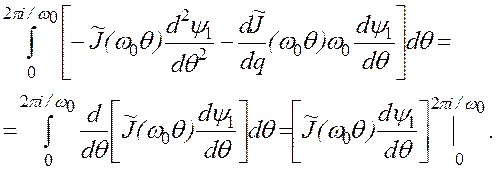             ,                                                        (2.73)

поскольку  - периодическая функция  с периодом . Во-вторых, интегрируя по частям, находим

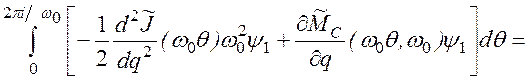
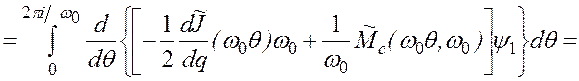
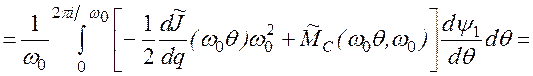
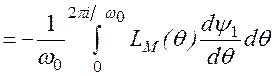.                                                                                                                (2.74)

Наконец, умножив уравнение (2.70) на  и проинтегрировав левую и правую части в пределах от 0 до , имеем

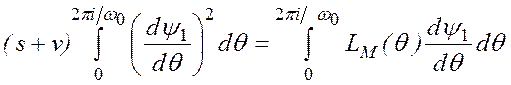,                                                                                                                 (2.75)

так как

.

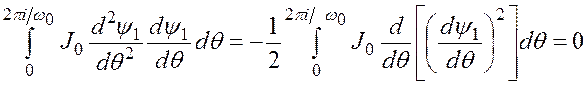Учитывая соотношения (2.73) - (2.75), приводим (2.72) к следующему виду:

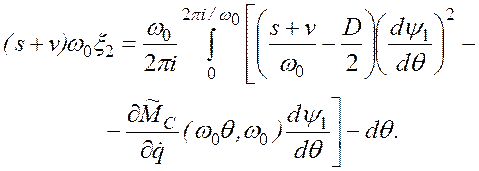                                                                                                                (2.76)

Если характеристики  и  являются линейными функциями  (D = 0), а  не зависит от , выражение (2.76) принимает более простой вид

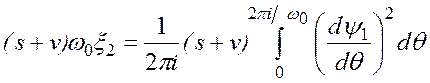.                                                                                                                (2.77)