Динамика жесткой машины с одной степенью подвижности, страница 16

Отметим, что [с учетом уравнения (2.70) и поскольку ] функция   не отличается от ранее введенной функции  
[см. (2.50)], поэтому в выражения (2.76) или (2.77) можно подставить последнюю, и производить интегрирование по t.

При выполнении условия (2.76) уравнение (2.71) имеет единственное частное периодическое решение, определяющее функцию .

Аналогичным путем, приравнивая в (2.63) члены порядка , можно определить  и , и продолжить процесс определения решения в форме (2.66). Доказано, что построенный таким образом степенной ряд (2.66) сходится к точному решению уравнения (2.63) при всех значениях , меньших некоторого  называемого радиусом сходимости ряда (2.66).

Поскольку исходное уравнение движения машины соответствует значению , важно, чтобы радиус сходимости был больше единицы. Определение радиуса сходимости является, однако, весьма сложной задачей. Обычно поэтому при применении метода малого параметра предположение о сходимости решения при  основывается на тех или иных физических соображениях. Хорошее представление о сходимости может дать сравнение функций  и , оценка их максимальных значений. Если добавочные члены в решении (2.66), появляющиеся в s-ом приближении, существенно меньше, чем члены s-1-го приближения, можно с уверенностью рассчитывать на сходимость процесса. Поскольку левые части дифференциальных уравнений, из которых определяются функции , одинаковы, представление о сходимости может дать сравнение правых частей. Сравнивая, например, правые части уравнений (2.70) и (2.71), можно установить, что максимальные значения членов, входящих в правую часть (2.71), относятся к максимальным значениям членов в правой части (2.70) приблизительно как . Приблизительно так же будут относиться и максимумы функций  и , т.е. второе приближение окажется мало отличающимся от первого.

Определение потерь энергии. При определении решения во втором приближении мы обнаружили, что средняя угловая скорость выходного звена двигателя будет отличаться от . Во втором приближении получаем из (2.67)

,

где      определяется из (2.76) или (2.77) и, как видно из этих выражений, зависит от . Таким образом, возникновение в системе колебательных процессов приводит к изменению средней угловой скорости машины.

Этому явлению нетрудно дать физическое объяснение. Действительно, колебательные процессы в любой системе обычно сопровождаются рассеянием энергии, которое может вызываться как силами сопротивления механического происхождения, так и сопротивлениями электрических контуров или гидравлическими сопротивлениями в двигателе. Поддержание установившегося движения машины требует поступления в систему дополнительной энергии, компенсирующей потери. Однако единственным источником энергии в машине обычно является двигатель; поэтому увеличение расхода энергии должно проявляться в увеличении нагрузки на двигатель, в результате чего появляется дополнительный средний момент сил сопротивления. Такой добавочный момент, вызванный колебаниями системы, называется вибрационным моментом. В первом приближении он определяется правой частью выражения (2.76):

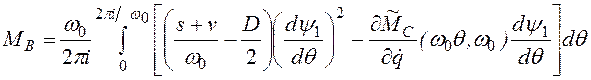 .                                                                                                                (2.78)

Умножив этот момент на коэффициент чувствительности , получим изменение средней угловой скорости двигателя.

Работу сил сопротивления за период, равную потерям энергии при колебаниях, можно получить, умножив момент [уравнение (2.78)] на угол поворота ротора двигателя, равный :

,

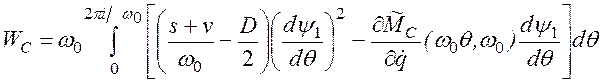или при D = 0,  = 0

.                                                                                                                (2.79)

Последнее уравнение можно непосредственно получить из уравнения (2.70). Из (2.75) следует, что в этом случае потери энергии равны работе возмущающей силы за цикл.

2.9.  Исследование установившегося движения

с учетом динамической характеристики двигателя

Определение средней угловой скорости. Условия устойчивости. Исследование установившегося движения машины с учетом динамической характеристики двигателя сводится к определению стационарного решения системы уравнении (2.15) и (2.17), в которой q и М_Д являются неизвестными функциями времени. Используя представления (2.7), (2.9), (2.14) и (2.18) и учитывая, что u = u₀ = const, перепишем эти уравнения в виде: