3) Разгружающее устройство и динамические гасители желательно располагать как можно ближе к источнику возмущений. В противном случае вся кинематическая цепь, состоящая из звеньев, расположенных между источником возмущений и разгружателем, оказывается нагруженной полным переменным моментом L(t).
2.8. Применение метода малого параметра.
Определение потерь энергии при колебаниях
Введение малого параметра в уравнение движения машины. При построении приближенного решения уравнения движения жесткой машины мы использовали метод последовательных приближений, основанный на предположении о близости закона движения выходного звена двигателя к равномерному вращательному движению. При этом оставался открытым вопрос о сходимости последовательных приближений к точному решению, о целесообразности определения высших приближений и т. п.
Попытаемся более подробно обосновать примененный метод решения, а также выявить некоторые важные свойства установившегося движения, вытекающие из анализа решения во втором приближении. С этой целью используем метод малого параметра, широко применяемый в различных задачах нелинейной механики. (А. Пуанкаре и А.М. Ляпунов). Ограничимся только теми сведениями, которые будут необходимы для решения уравнения движения жесткой машины.
Обратимся вновь к уравнению (2.28). Как уже
отмечалось, в правую часть этого уравнения вынесены те члены, присутствие
которых вызывает отклонение закона движения q(t) от равномерного вращения. Поскольку разыскиваются
движения, близкие к равномерному вращению, есть основания считать, что при этих
движениях правая часть уравнения (2.28) должна оставаться малой по величине.
Принимая во внимание это предположение, введем в правую часть уравнения
множитель ![]() ,
т.е. запишем уравнение в следующем виде:
,
т.е. запишем уравнение в следующем виде:
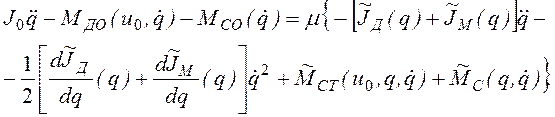 (2.62)
(2.62)
Множитель ![]() , называемый малым параметром, может
принимать любые положительные значения. Введя его, мы тем самым вместо одного дифференциального
уравнения получили семейство уравнений, причем уравнение (2.28) является одним
из уравнений этого семейства, соответствующим значению
, называемый малым параметром, может
принимать любые положительные значения. Введя его, мы тем самым вместо одного дифференциального
уравнения получили семейство уравнений, причем уравнение (2.28) является одним
из уравнений этого семейства, соответствующим значению ![]() . Для каждого значения
. Для каждого значения ![]() уравнение
(2.62) может иметь стационарное решение, которое, таким образом, оказывается
функцией параметра
уравнение
(2.62) может иметь стационарное решение, которое, таким образом, оказывается
функцией параметра ![]() .
.
Основная идея метода состоит в отыскании решения в виде степенного ряда по малому параметру.
Определение порождающего решения. С процедурой отыскания решения ознакомимся на
примере уравнения (2.62). Для упрощения дальнейших выводов примем, что ![]() и
и ![]() т. е.
что источником возмущения является только механическая система машины. В этом
случае уравнение (2.62) запишется в виде
т. е.
что источником возмущения является только механическая система машины. В этом
случае уравнение (2.62) запишется в виде
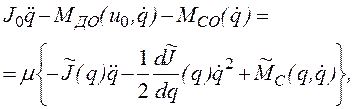 (2.63)
(2.63)
где ![]() и
и ![]() периодические
функции q с периодом 2pi.
периодические
функции q с периодом 2pi.
Решения уравнения (2.63), близкие к режиму равномерного вращения, разыскиваются в виде ряда
![]() (2.64)
(2.64)
где ![]() - средняя угловая скорость,
подлежащая определению в процессе решения;
- средняя угловая скорость,
подлежащая определению в процессе решения; ![]() —
неизвестные периодические функции с периодом 2pi/w.
—
неизвестные периодические функции с периодом 2pi/w.
При m = 0 получаем уравнение
![]() ,
,
которое называется порождающим уравнением семейства (2.63). Как было показано выше, это уравнение, вообще говоря, имеет одно или несколько решений вида
![]() , (2.65)
, (2.65)
в котором ![]() определяется из условия (2.27)
определяется из условия (2.27) ![]() . Решения (2.65) называются порождающими
решениями семейства уравнений (2.63). Выбрав одно из них, в дальнейшем будем
искать близкое к нему решение вида (2.64). При этом последовательно найдем
функции
. Решения (2.65) называются порождающими
решениями семейства уравнений (2.63). Выбрав одно из них, в дальнейшем будем
искать близкое к нему решение вида (2.64). При этом последовательно найдем
функции ![]() (s = 1, 2,
...) и уточним значения
(s = 1, 2,
...) и уточним значения ![]() .
.
Определение решения в первом и втором приближениях. Неизвестный
период функций ![]() равен, очевидно
равен, очевидно ![]() , где
, где ![]() -
величина, которая должна определяться в процессе решения. Чтобы не искать функции,
период которых неизвестен, применим следующий прием, предложенный
А.М.Ляпуновым. Будем искать период
-
величина, которая должна определяться в процессе решения. Чтобы не искать функции,
период которых неизвестен, применим следующий прием, предложенный
А.М.Ляпуновым. Будем искать период ![]() в виде ряда по степеням
в виде ряда по степеням
![]() :
:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.