Анализ линейных систем автоматического управления: Методическое пособие по дисциплине "Теория автоматического управления", страница 6

У преобразования Фурье, наряду с его очевидными достоинствами, есть существенный недостаток: это преобразование можно применить только к абсолютно интегрируемым функциям. Чтобы расширить область абсолютно интегрируемой функции Лаплас умножил оригинал на динамический коэффициент , но при этом интервал интегрирования определил  и  . После таких дополнений преобразование Фурье приняло вид

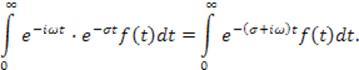
Обозначив  , получим выражение, определяющее преобразование Лапласа

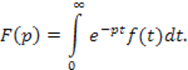
Для определения оригинала можно воспользоваться обратным преобразованием Лапласа

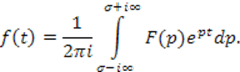
Как и в случае с преобразованиями Фурье каждому значению преобразования Лапласа  соответствует вполне определенное и единственное значение оригинала .

2.4.1. Изображение элементарных функций

Преобразования Лапласа являются основой операционного исчисления. В операционном исчислении принято функцию  называть оригиналом; функцию  называть изображением.

Если функция  есть изображение функции , то это символически выглядит следующем образом:                  или    или  .

Функция Хевисайда

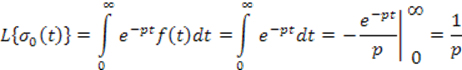
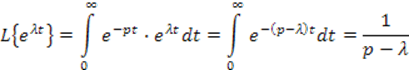
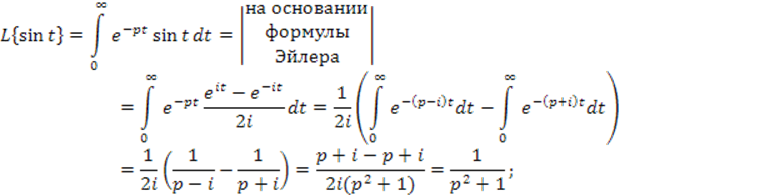
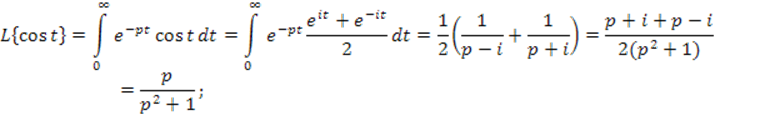
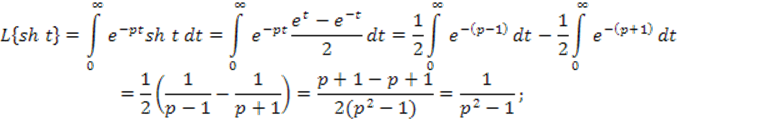
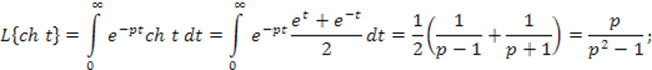
Свойства преобразования Лапласа

1.  Линейность преобразования.

Теорема 1:

Если ; ;…;  и  - величина не зависящая от pиt, то справедливо равенство

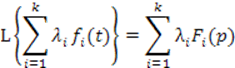
Теорема очевидна. Интеграл суммы есть сумма интегралов, а постоянный множитель можно вынести за знак интеграла

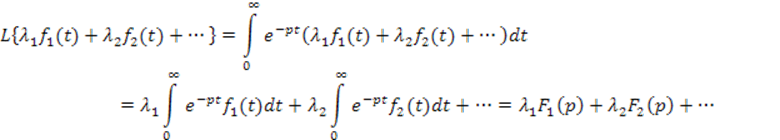
2.  Линейность смещения

Теорема 2:

Если функция   имеет изображение , то  , будет иметь изображение .

Для доказательства найдем изображение

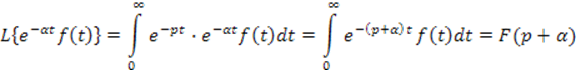
Таким образом .

Пример:

Т.к   , то по теореме смещения:

Аналогично можно определить смещение синуса:

Теорема 3:

Если функция   имеет изображение , то изображение смещенного оригинала  будет иметь вид:

Для доказательства воспользуемся определением преобразования Лапласа.

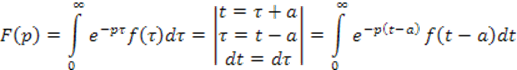
Умножим левую и правую части полученного выражения на .

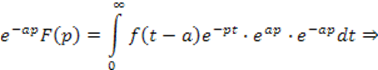
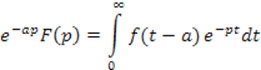
Но тогда правая часть последнего выражения есть, по определению, изображение Лапласа функции . И это изображение равно:

Что и требовалось доказать.

3.  Изображение производной

Теорема 4:

Если функция   имеет изображение , то изображение производной функции  будет определяться выражением

Доказательство этой теоремы следует из определения преобразования Лапласа:

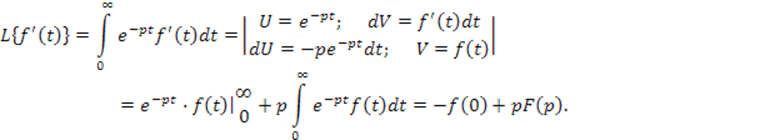
Теорема доказана.

Замечание

На основании доказанной теоремы можно найти изображение для производной любого порядка.

В общем виде  изображение производной любого порядка будет иметь вид

                                     .

4.  Дифференцирование изображения

Теорема 5:

Если функция   имеет изображение , то производная от изображения  соответствует

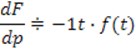
Для доказательства продифференцируем изображение по Лапласу:

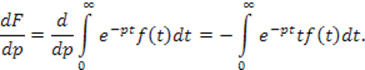
Полученное вырожение соответствует изображению функции  Что и требовалось доказать.

Замечание1.

Производная n-го порядка от изображения соответствует функции  .

Пример:

С помощью теоремы дифференцирования определим изображение функции .

Функция Хевисайда имеет вид

Ее изображение

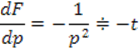
Или

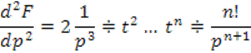
5.  Изображение интеграла

Теорема 6:

Если функция  имеет изображение , то

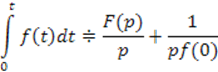
Для доказательства воспользуемся определением преобразования Лапласа

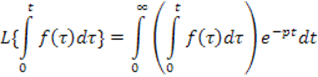
Известно, что несобственный интеграл

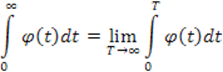
Тогда

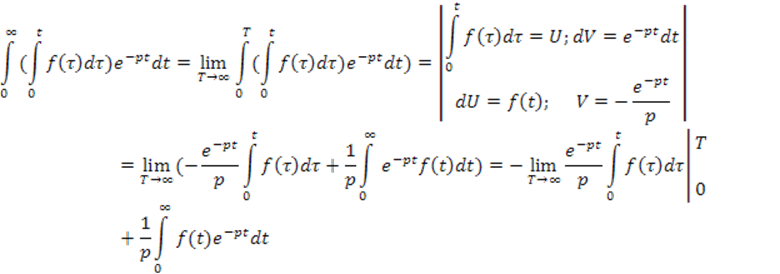
Первое слагаемое последнего выражения равно нулю. Второе есть   .

Что и требовалось доказать.

Теорема 7 (свертывания):

Если  и , то

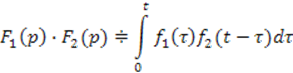
Для доказательства найдем изображение

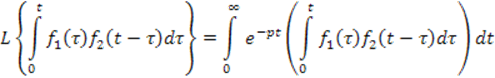
В правой части выражения находится двукратный интеграл, который берется по области, ограниченной линиями .

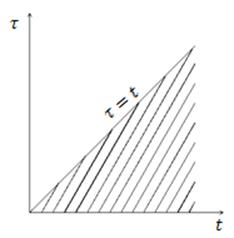Изменим порядок интегрирования.

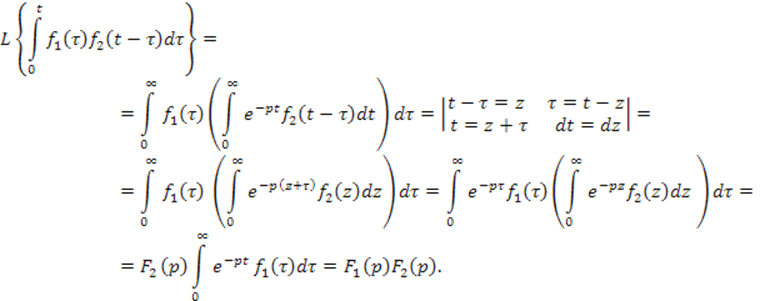
3.  АНАЛИЗ ЛИНЕЙНЫХ НЕПРЕРЫВНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

3.1.  Передаточная функция САУ

Математическую модель линейной стационарной динамической системы можно представить в виде линейно дифференциального уравнения n-го порядка

Левая часть последнего уравнения есть математическая модель собственного поведения системы. Правая часть – внешние воздействия (как правило через U обозначается внешние управляющие воздействия).

 – функция, определяющая состояние системы (неизвестная функция):

 – коэффициенты (параметры) системы (будем считать, что они не меняются во времени).