В установившемся состоянии (после окончания переходного процесса) модель будет описываться алгебраическим уравнением вида:
F(x0) = φ(g0),
Где x0 и g0 - установившиеся значения векторов состояния и внешнего воздействия
Исследование нелинейных систем сопряжено с серьезными математическими трудностями. Чтобы эти трудности уменьшить, математическую модель системы, если она не является существенно нелинейной, линеаризуют. При этом полагают, что отклонение вектора состояния системы от установившегося значения – мало.
Обозначим указанные отклонения через Δх(t). Тогда
х = х0 + Δх, х’ = х0’ + Δх’ , … , x(n) = х0(n) + Δх(n).
Обычно для систем с отрицательной обратной связью условие малости отклонения выполняются.
Разложим правую часть выражения (2.1) в ряд Тейлора в окрестности х0, ограничившись линейными членами разложения.
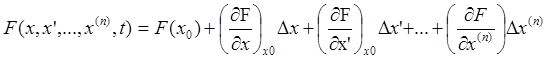
Найдем разность между динамическим и статическим состояниями системы.
![]() -
- ![]() =
=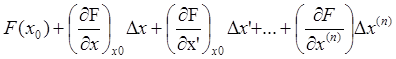 -
-![]() =
= 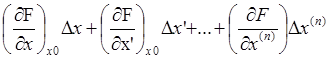
Проделав аналогичные операции с правой частью, получим уравнение системы в конечных разностях
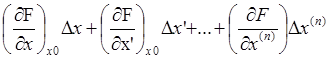 =
=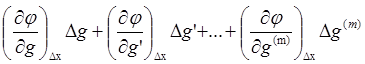
На практике знак Δ опускают, а частные производные обозначают: в левой части коэффициентами a(t); в правой – b(t).
![]() ,
,
где
аibj - соответствующие частные производные при фиксированных в момент времени t0значениях вектора состояния системы;
х - состояние системы;
u - внешнее воздействие.
В общем случае коэффициенты аibj являются функциями, зависящими от времени, но при малых отклонениях состояния системы от установившихся значений их можно считать постоянными величинами не допуская при этом заметной ошибки.
![]() , (2.2)
, (2.2)
При использовании
математической модели удобней представить ее не одним уравнением n – го порядка, а системой, состоящей
из n уравнений 1- го порядка. Для
этого обозначим:
x = x1; x’ = x2; …; x(n-1) = xn;; u = u1; u’ = u2;…u(m-1) = um+1.
С учетом принятых обозначений исходное уравнение в форме Коши запишется в виде:
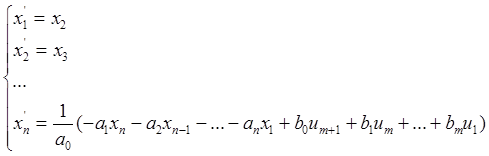
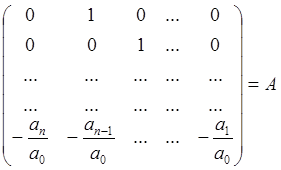 ;
; 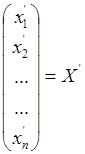 ;
; 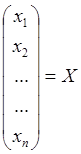
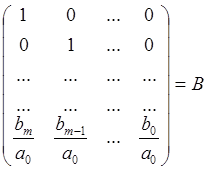
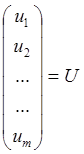
тогда
Для примера рассмотрим RC – цепочку, состоящую из резистора и
емкости
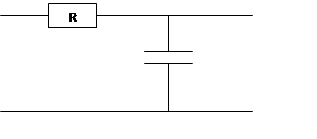
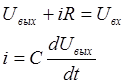
Здесь
Uвх – входное напряжение цепи
Uвых – выходное напряжение цепи
I – ток цепи
С – емкость конденсатора
Подставим полученное значение тока в исходное уравнение и предположим, что U(t)=0, получим
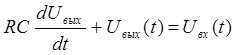
Поведение САУ во временной области описывается или с помощью дифференциальных уравнений n – го порядка.
![]() ,
,
или с помощью систем уравнений
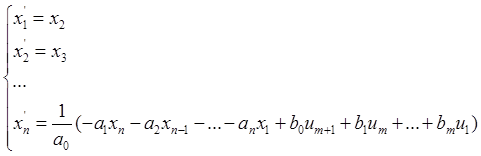
или в матричной форме
![]()
Если правая часть уравнения (2.2) равна нулю (однородное уравнение), то это есть математическая модель поведения системы без внешних воздействий на нее.
Если математическая модель системы представляет собой дифференциальное уравнение первого порядка, то ее исследование можно провести, найдя общее решение этого уравнения. Сделать это можно различными способами. Например, использую метод Бернулли.
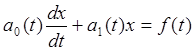 (2.3)
(2.3)
![]()
![]() (2.4)
(2.4)
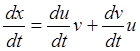
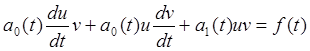
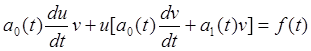 (2.5)
(2.5)
Так как один из сомножителей (2.4) можно выбрать любым, то пусть v(t) будет таким, чтобы в последнем выражении величина, заключенная в квадратные скобки была равна нулю.
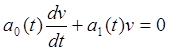
Последнее выражение есть дифференциальное уравнение с разделяющимися переменными
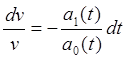
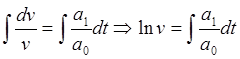
![]()
После подстановки полученного значения v в уравнение (2.5) последнее примет вид:
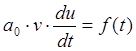
Это есть уравнение первого порядка с разделяющимися переменными, решение которого можно представить как
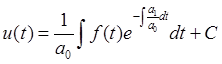 .
.
В окончательном виде общее решение дифференциального уравнения (2.3) будет выглядеть как
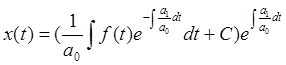
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.