2.23. Статистическая сумма спина в поле равна
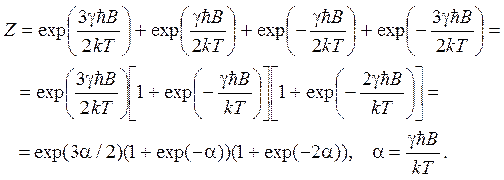
Отсюда
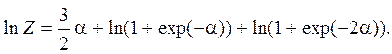
Находится средняя энергия спина
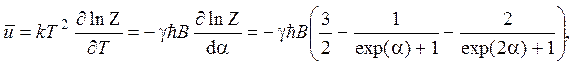
где 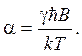
3.1. Если газ не очень
плотный, то при расчете частоты столкновений следует учитывать только парные
столкновения (столкновениями одновременно более чем двух молекул можно
пренебречь). При этом молекулы в некотором приближении можно считать упругими
шариками. Если ![]() и
и ![]() –
скорости двух молекул, то для столкновения важны не сами по себе эти скорости,
а скорость относительного движения молекул
–
скорости двух молекул, то для столкновения важны не сами по себе эти скорости,
а скорость относительного движения молекул
![]()
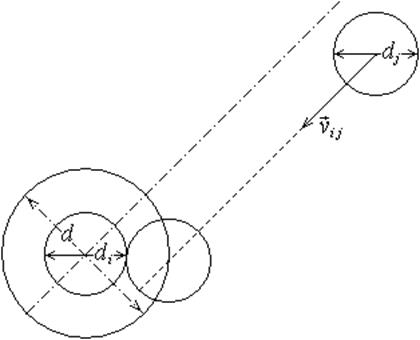
Задача решается в системе отсчета, связанной с рассматриваемой молекулой. Все остальные молекулы движутся с относительными скоростями и, как известно, распределены по скоростям с вероятностью, определяемой распределением Максвелла, в которое входит приведенная масса молекул m.
Вместо рассматриваемой молекулы можно ввести гипотетическую частицу диаметром d = di + dj, где di и dj – диаметры сталкивающихся молекул, заменив все остальные молекулы материальными точками. Таким образом, задача определения частоты столкновений сводится к нахождению числа ударов о круг диаметром d частиц максвелловского газа. Она равна произведению плотности потока двумерного газа (см. задачу 2.9) на длину окружности. Для частоты столкновений молекулы i -го сорта с молекулами j -го сорта получаем
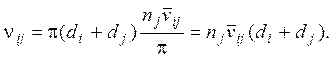
Здесь ![]() –
средняя относительная скорость. Она вычисляется по той же формуле, что и просто
средняя скорость теплового движения молекул двумерного газа, только с заменой
массы молекулы на приведенную массу, поскольку характер распределения молекул
по скоростям один и тот же (распределение Максвелла).
–
средняя относительная скорость. Она вычисляется по той же формуле, что и просто
средняя скорость теплового движения молекул двумерного газа, только с заменой
массы молекулы на приведенную массу, поскольку характер распределения молекул
по скоростям один и тот же (распределение Максвелла).
 |
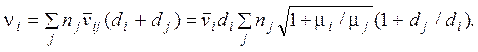
В случае наличия только одного сорта частиц частота столкновения молекулы равна
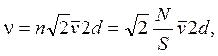
где
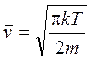 – средняя скорость теплового движения
молекул двумерного газа.
– средняя скорость теплового движения
молекул двумерного газа.
В действительности молекулы взаимодействуют не только при непосредственном соприкосновении, но и при пролете на некотором расстоянии друг от друга. Такой характер взаимодействия обычно учитывается посредством введения эффективного сечения столкновения.
3.2. Будем считать, что газ только диффундирует. Тогда его концентрация будет удовлетворять уравнению
¶n/¶t = DDn + b,
где D – лапласиан. В стационарном случае производная по времени равна нулю. Задача обладает осевой симметрией. Кроме того, тело длинное, и можно не учитывать зависимость концентрации газа от координаты вдоль оси тела. В результате уравнение упрощается и принимает вид
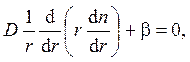
где r – радиус цилиндрической системы координат.
Решение этого уравнения должно удовлетворять граничным условиям:
r = 0 çdn/dtç < ¥,
r = Rn= 0.
Однократное интегрирование дает
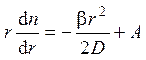
С учетом первого граничного условия постоянная А = 0, и уравнение сводится к виду
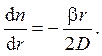
Последующее интегрирование с учетом второго граничного условия дает распределение концентрации газа в теле
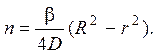
3.3. Поток тепла через толщу льда постоянный в силу стационарности задачи и равен заданной величине q. С градиентом температуры он связан законом Фурье
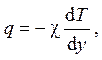
где координата y направлена вверх от нижней поверхности льда. Интегрирование этого уравнения не должно вызывать трудностей. С учетом того, что абсолютная температура нижней поверхности льда равна 273 К (температура замерзания воды), получаем
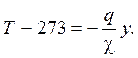
Температура воздуха задана. Для установившейся толщины льда получаем формулу
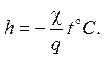
3.4. По закону Фурье плотность потока тепла
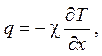
где коэффициент теплопроводности
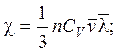
CV – теплоемкость в расчете на одну молекулу (можно считать CV постоянной); длина свободного пробега
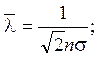
s – сечение столкновения (в первом приближении s также не зависит температуры); средняя скорость теплового движения
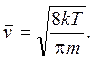
Таким образом,
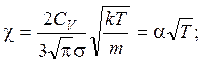
Так как задача стационарная, то поток тепла через любое сечение столба газа остается постоянным, т.е.
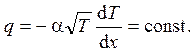
Интегрирование этого уравнения дает распределение температуры по длине столба:
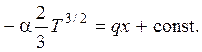
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.