Электропроводность электролитов. Диффузия в электролитах. Компьютерное моделирование ионной атмосферы, страница 5

Современ­ная теория растворов электролитов основана на том, что в растворе сохраняется присущее кристаллам распределение ионов, при котором каждый из них окружен преимущественно ионами про­тивоположного знака. Однако в растворах, в отличие от кристаллов, тепловое движение ионов приводит к тому, что они не сохраняют своего фиксированного положения в узлах кристаллической решет­ки, а располагаются вокруг выбранного центрального иона в виде сферы. Исходя из того, что в растворе основным видом движения является поступательное (а не колебательное, как в кристаллах), одни и те же ионы не могут постоянно входить в состав сферы, окружающей центральный ион. Они непрерывно обмениваются своими местами с другими ионами. Такая статистическая сфера, окружающая центральный ион, называется ионной атмосферой. Все ионы раствора равноправны, каждый из них окружен ионной атмосферой и в то же время каждый центральный ион входит в состав ионной атмосферы какого-либо другого иона (рис. 5). Существо­вание ионных атмосфер и есть тот характерный признак, который по Дебаю и Гюккелю отличает реальные растворы электролитов от идеальных. Дополнительная энергия G* реальных растворов

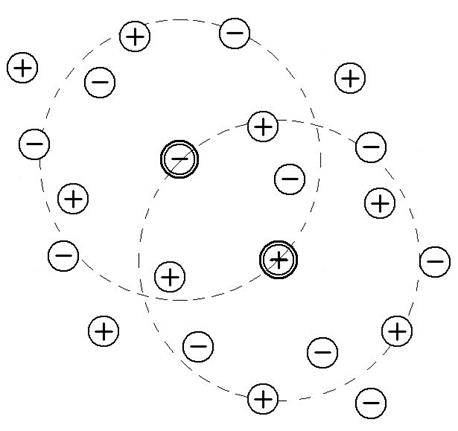
Рис.5. Модель ионной атмосферы, принятая теорией Дебая и Гюккеля.

должна поэтому отражать эф­фект суммарного действия ионных атмосфер на централь­ные ионы. Расчет энергии межионного взаимодействия и коэффици­ентов активности. Энергия, связанная с ионной атмосфе­рой,— электрическая, поэто­му она должна быть функцией плотности электрического за­ряда и потенциала, созда­ваемых ионной атмосферой. Так как последняя представ­ляет собой статистическое образование, можно не учитывать дискретное распределение заря­дов и использовать уравнение Пуассона для связи между сред­ней плотностью заряда ρ и отвечающей ему средней величиной потенциала j

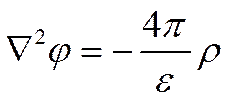                                                                    (I I-31)

где e—диэлектрическая  постоянная;   а  Ñ²—оператор  Лапласа, который можно выразить в  прямоугольных  координатах

                                                       (I I - 32)

В уравнение Пуассона входят две неизвестные величины — ρ и j. Чтобы их найти, необходимо иметь второе уравнение, связы­вающее обе эти переменные. Дебай и Гюккель получили нужное уравнение следующим образом.

Пусть объем раствора равен V, полное число ионов первого сорта равно N₁второго — N₂, i-го — N_iи последнего — N_h, а их заряды равны соответственно ez₁ , ez₂ , ez_iи ez_k. Так как число зарядов положительных и отрицательных ионов электролита одина­ково, то

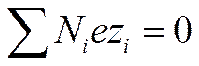   И 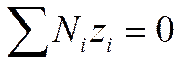                                           (I I - 33)

Закон электронейтральности справедлив не только для раствора в целом, но и для любого заданного элемента его объема, доста­точно большого по сравнению с размерами иона. Если выбран объем раствора, равный единице, то

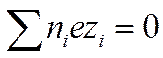 И 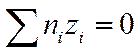    (I I -34)

Рис.6. Схема распределения зарядов в поле центрального иона.

где n₁—число ионов i-го сорта в единице объема (на­пример, в 1 мл). Однако заряд некоторого элемента объема dV, находящегося вблизи какого-либо иона и перемещающегося вместе с ним во время теплового движения внутри раствора (рис. 6), будет отличаться от нуля вследствие сущест­вования ионной атмосферы. Если центральный ион, расположенный в начале координат, заряжен поло­жительно, то элемент объ­ема dVбудет обладать из­быточным отрицательным зарядом. Предполагая, что к распределению ионов в растворе при­меним принцип Больцмана и что силы, действующие между ионами, по своей природе электростатические, число отрицательных ионов в элементарном объеме dVможно выразить как

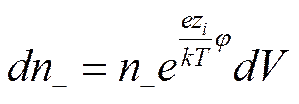
а число положительных

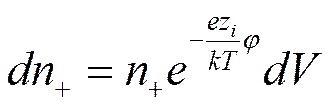
Заряд элемента объема будет равен тогда

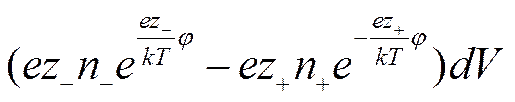
а плотность заряда

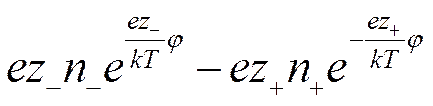
Учитывая, что в растворе находятся различные сорта ионов, и приписывая валентности иона знак, отвечающий его заряду, можно написать, что

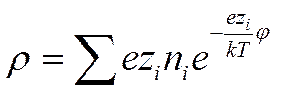                                     (I I -35)

Подставим величину ρ из выражения (II-35)  в  уравнение  Пуас­сона

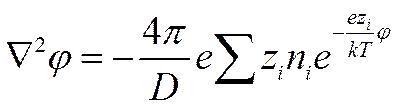                                      (I I-36)