Кратные интегралы, страница 3

Вопрос 5. Вычисление двойных интегралов двумя последовательными интегрированиями (общий случай).

Пусть S – стандартная область в направлении оси Оy и ограничена сверху графиком функции y=y₂(x), снизу – y=y₁(x). И пусть R={(x,y): a≤x≤b, c≤y≤d}, причем это минимальный прямоугольник, в котором содержится область S.

Пусть в области S ограничена и непрерывна функция z=f(x,y). Введём новую функцию: .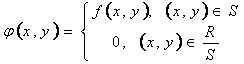

Отсюда следует 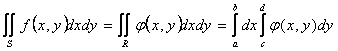, где 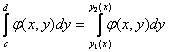, где y₁(x) и y₂(x) – фиксированные числа.

Тогда получаем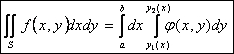

.

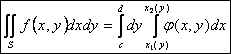Вопрос 6. Замена переменных в двойном интеграле.

Для того чтобы преобразовать двойной интеграл, заданный в декартовых координатах, в двойной интеграл в криволинейных координатах, нужно заменить в подынтегральной функции z=f(x,y) переменные x и yсоответственно через x=φ(u,v), y=ψ(u,v), а элемент площади dxdy– его выражением в криволинейных координатах: dxdy=|I|dudv, где I – якобиан, который равен 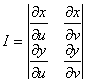.  - формула замены переменных в двойном интеграле.

Вопрос 7. Якобиан, его геометрический смысл.

Определитель

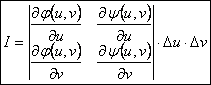
называется функциональным определителем функций φ(u,v), ψ(u,v) или якобианом. Величина якобиана играет роль локального коэффициента растяжения области S' (в данной точке (u,v)) при отображении ее на на область S при помощи формул преобразования: .

Вопрос 8. Двойной интеграл в полярных координатах.

Чтобы преобразовать двойной интеграл в декартовых координатах в двойной интеграл в полярных координатах, нужно x и y в подынтегральной функции заменить соответственно через rcosφи rsinφ, а элемент площади в декартовых координатах dxdy заменить элементом площади в полярных координатах rdrdφ, где r≥0, 0≤φ≤2π.