Розподільчий закон 8 дозволяє скоротити кількість елементів, потрібних для виконання логічних функцій (рис. 2.2,а,б). Якщо для функції АБО він є звичний,
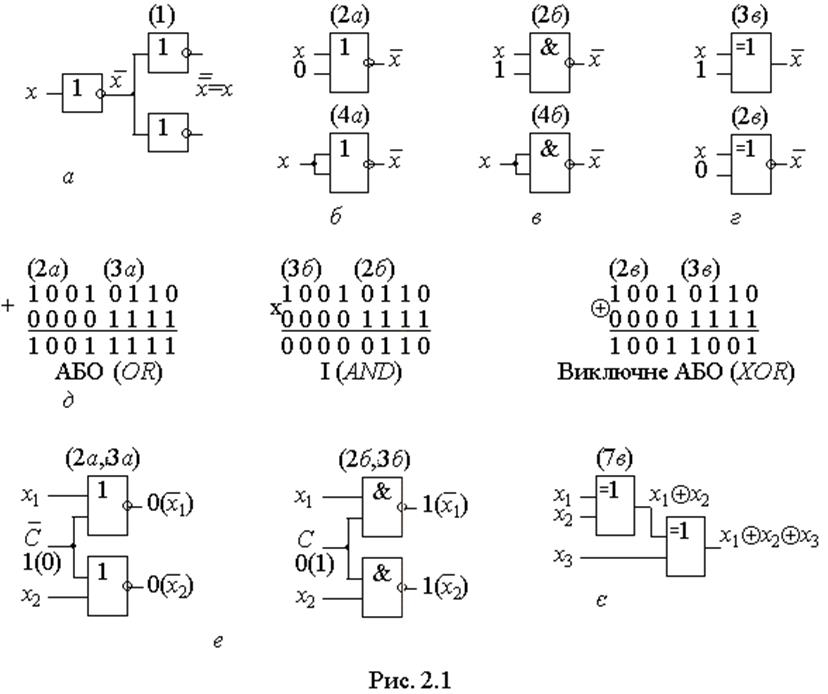
то для функції І має форму, відсутню в звичайній алгебрі. Перевірити формулу 8б, як і інші співвідношення, можна методом прямої індукції: підставляючи у формулу всі можливі комбінації змінних, наприклад, за таблицею відповідності, переконуємося в рівності лівої та правої частин виразу для кожного набору змінних.
Інший шлях доведення (який застосовується також для спрощення функцій) – методом тотожних перетворень зводимо одну частину рівності до іншої. Для стислості будемо під елементами виразу зазначати нумерацію співвідношеннь, на підставі яких зроблені перетворення. Для розподільчого закону 8б маємо:
х1+х2х3=х1.1+х2х3=х1(1+х2+х3)+х2х3=(х1+х1х2+х1х3)+х2х3=
2б 3а 8а
=х1х1+х1х2+х1х3+х2х3=(х1+х2)·(х1+х3),
4б 8а
що й треба було довести.
Закони двоїстості 9 (закони інверсії,
правила або закони де Морґана) для зручності записано в двох формах на підставі
аксіоми 1. Із цих законів випливає двоїстість елементів АБО та І (рис. 2.2,в,г).
У позитивній логіці, якою ми користуємось за угодою (за умовчанням вважаємо,
що завжди лог. 1 кодується висо- 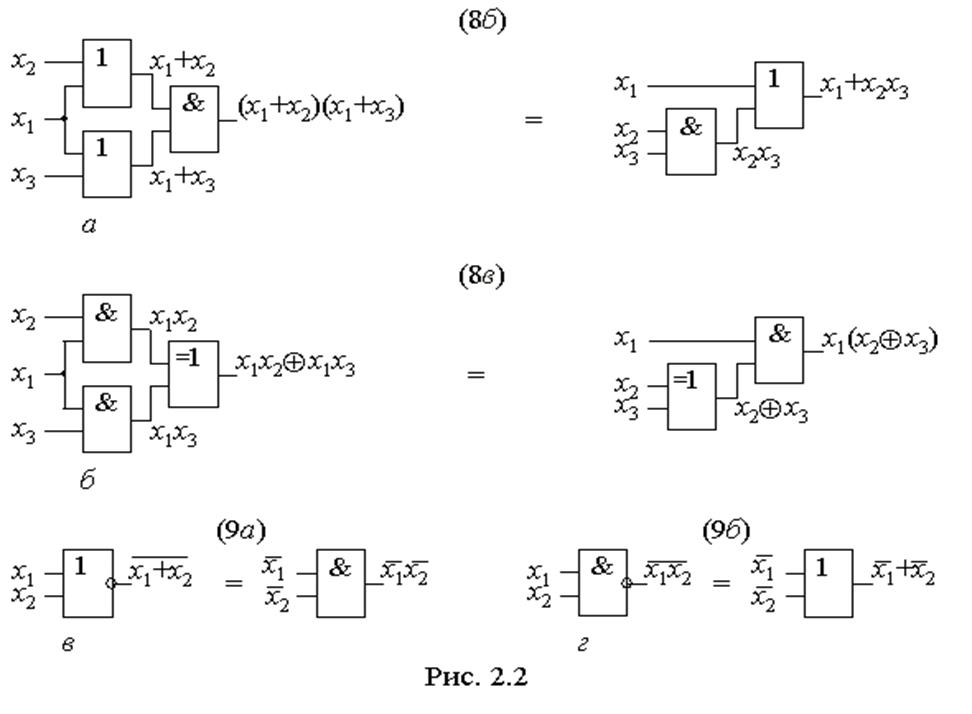
ким рівнем напруги, а лог. 0 – низьким), елементи АБО та І виконують однойменну логічну функцію, проте в негативній логіці (лог. 1 – відповідає низькому рівневі напруги, а лог. 0 – високому), навпаки, елемент АБО можна вважати елементом збігу нулів на його входах (при цьому на виході буде теж нуль), а елемент І – елементом збирання нульових сигналів (на його виході є нуль, якщо хоча б один з аргуметів нульовий). Із законів де Морґана можна зробити корисне узагальнення:
![]() (2.1)
(2.1)
тобто взаємна заміна в логічному виразі будь-якої функції y прямих і інверсних змінних та знаків логічного додавання і множення
спричиняє її заперечення. Наприклад, 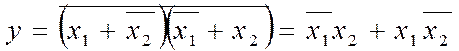
3. Наслідки. Слід відзначити, що закони 6...9 дійсні для довільної кількості аргументів. Це стосується й наслідків 10...12, які часто вживаються для спрощення функцій, їх синтезу, інших тотожних перетворень. Проте процес перетворень залежить від індивідуального підходу, досвіду тощо. Про це свідчить, наприклад, доведення наслідку 12а двома шляхами:
1)![]()
![]()
![]()
(2.1) (8a) (5б) (9а) 1
2) ![]()
(8б) (5а) (2б)
Таким чином, перетворення логічних функцій та схем виконуються за розглянутими співвідношеннями алгебри логіки. На відміну від звичайної, у булевій алгебрі всі співвідношення симетричні відносно функцій логічного додавання та множення. Аби запобігти помилок щодо послідовності виконання операцій, слід діяти за погодженням: найстаршою є операція логічного заперечення (бо заперечення суми аргументів не дорівнює сумі їх заперечень), за нею йде логічне множення і найнижчою є операція логічного додавання. Послідовність дій можна змінити, як звичайно, за допомогою дужок. З огляду на аксіоми 4а,б в алгебрі логіки множення на коефіцієнти, відмінні від 0 та 1, а також піднесення до степеня не мають сенсу.
Тотожні перетворення, особливо складних логічних виразів, для їх спрощення доцільно виконувати формалізованими методами й лише після цього, у разі потреби, завершувати ручним способом.
2.1.4. Стандартні форми логічних функцій
1. Означення. Шляхом тотожних перетворень за законами алгебри логіки можна утворити безліч еквівалентних булевих виразів будь-якої функції. Аби вибрати з-поміж них оптимальну та алгоритмізувати процес перетворень, вдаються до надання логічним виразам стандартної форми.
Для прикладу розглянемо логічну функцію, зображену в таких еквівалентних формах:
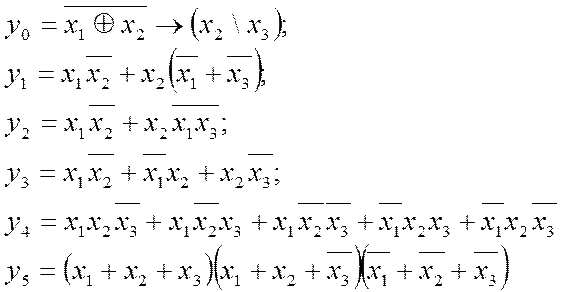
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.