![]()
і диз'юнкцію D12=y1+y2 (див. діаграму D12)
![]()
на основі яких за (2.9) дістаємо вираз другої функції
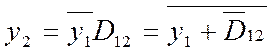
та реалізуємо обидві функції y1, y2 спільно на трьох елементах (схемну реалізацію без додаткових посилань див. на рис. 2.14,в).
Якщо вважати функцію у3 відомою, так само можна мінімізувати неперетинну з нею функцію у5. Для цього об'єднанням одиниць з діаграм y3 і y5 будуємо діаграму D35=y3+y5 (див. рис. 2.14,б) та мінімізуємо диз'юнкцію. Неважко помітити, що функція y2 перетворюється в D35 додаванням до неї нижнього рядка одиниць, тобто D35=y2+x3. Тоді

отже, функція y5 реалізується на двох елементах АБО-НЕ.
б) Включення шуканої функції до складу відомої. За спільної мінімізації функцій y2 і y3 має місце випадок y3 Ì y2, бо діаграма y3 є частиною діаграми y2. Як і в попередньому випадку, маємо згідно з (2.10) теж 3 складники: y2, y3 та R23=y2\y3, отже, діємо в такий самий спосіб. Простішу функцію y2 вже визначено, тому будуємо діаграму для різниці вилученням одиниць із тих клітинок діаграми y2, що збігаються з одиницями діаграми y3 (див. діаграму R23), що еквівалентно вилученню з діаграми y2 нижнього рядка, тобто x3:
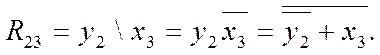
Відтак, згідно з (2.10) функцію
![]()
реалізуємо елементом І.
в) Включення відомої функції до складу шуканої. За спільної мінімізації функцій y3 і y4 ситуація зворотна попередній: тепер функція y3, яку вважаємо відомою, є частиною шуканої, тобто y3Ì y4, що видно безпосередньо з діаграм.
Тому, згідно з (2.11), будуємо діаграму для різниці R43=y4\y3, яка збігається з діаграмою y1, тобто R43=y1, отже, маємо реалізацію на елементі АБО:
![]()
Очевидно, такий самий результат можна дістати, якщо за відому функцію взяти y1, бо тоді різниця становитиме R41=y4\y1=y3; отже, y4=y1+R41=y1+y3.
г) Інверсія. Безпосередньо з
таблиці відповідності видно, що останні дві функції є інверсії вже відомих ![]() ,
, ![]() і найпростіше
реалізуються за допомогою інверторів. Проте такий спосіб пов'язаний із
погіршенням швидкодії (п.2.4.3). У разі неприйнятності цього утворюють обернені
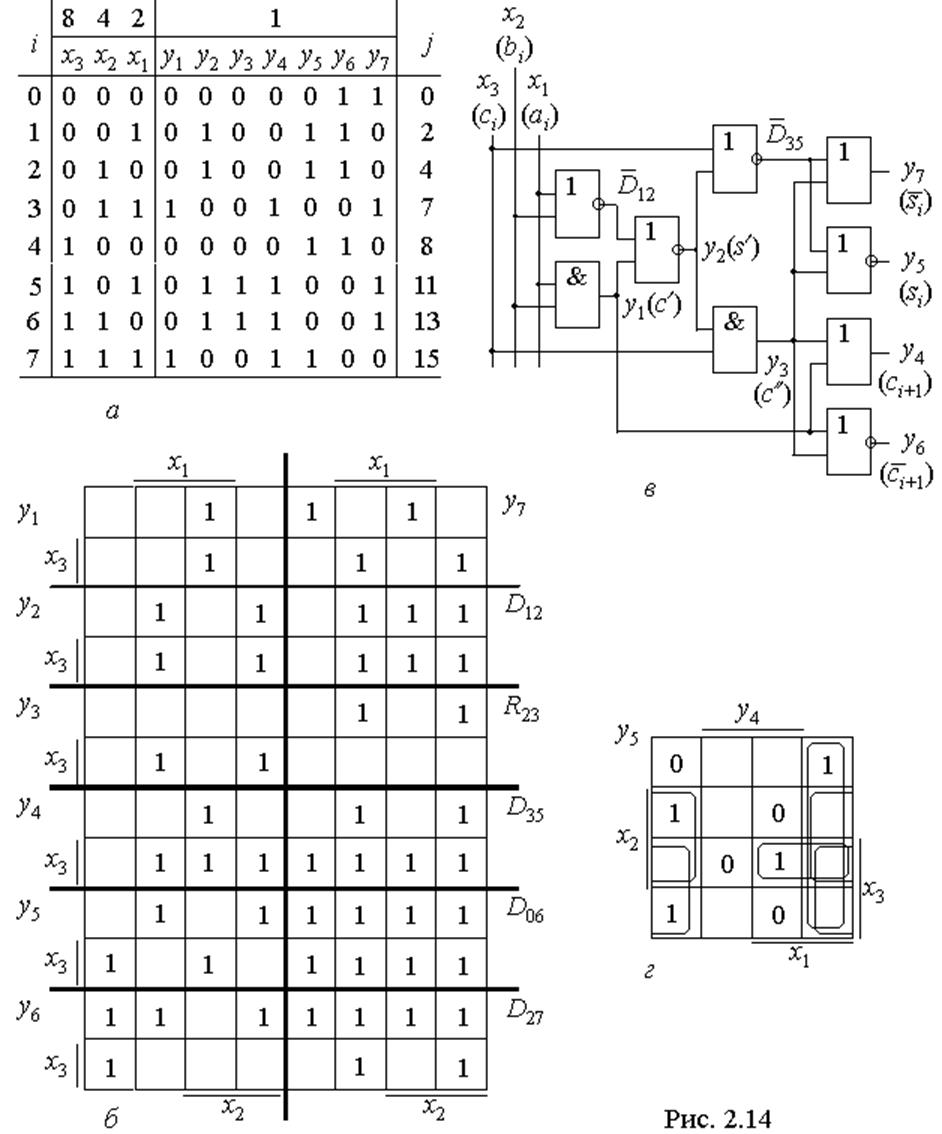
функції y6=°y4, y7=°y5, які є логічно еквівалентні інверсіям
і найпростіше
реалізуються за допомогою інверторів. Проте такий спосіб пов'язаний із
погіршенням швидкодії (п.2.4.3). У разі неприйнятності цього утворюють обернені
функції y6=°y4, y7=°y5, які є логічно еквівалентні інверсіям ![]() ,
, ![]() , але формуються
окремо, аналогічно прямим функціям. У загальному випадку,
коли функції є частково визначеними,
вони можуть довизначатися по-
, але формуються
окремо, аналогічно прямим функціям. У загальному випадку,
коли функції є частково визначеними,
вони можуть довизначатися по-
різному при синтезі прямих
і обернених функцій з метою спрощення виразів. Внаслідок цього
вирази для °y і ![]() можуть
не зводитись один до одного шляхом тотожних перетворень. У цьому й полягає різниця
між оберненою і інверсною функціями. Розглянемо синтез функцій y6,
y7 як обернених до y4, y5.
можуть
не зводитись один до одного шляхом тотожних перетворень. У цьому й полягає різниця
між оберненою і інверсною функціями. Розглянемо синтез функцій y6,
y7 як обернених до y4, y5.
д) Використання кількох функцій. Інколи кращий результат спільної реалізації можна дістати, якщо під час синтезу шуканої функції за відому правитиме якась композиція (кон'юнкція, різниця тощо) кількох вже відомих функцій. Прикладом є використання такої композиції для синтезу функції y6, коли за відому функцію правитиме об'єднання D12=y1+y2 (див. діаграму), яке позначимо y0=D12.
е) Суцільне покриття області визначення. При цьому маємо випадок, коли об'єднання шуканої і відомої функцій D06=y6+D12=1 покриває всю діаграму одиницями (див. рис. 2.14,б), а їх перетин y6D12 ¹0 відмінний від нуля. На підставі (2.8) визначаємо різницю R06=D12\y6, діаграма якої збігається з діаграмою y4, що в свою чергу утворюється об'єднанням y1 та y3. Отже, функція
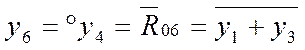
реалізується елементом АБО-НЕ.
є) Загальний випадок співвідношення функцій. Якщо для синтезу функції y7 скористатися вже реалізованою функцією y2, то за ознаками D27=y2+y7 ¹1, K27=y2y7 ¹0 маємо загальний випадок їх
співвідношення. Вибираючи варіант виразу (2.7), синтезуємо D27 і K27. Діаграму D27 (див. рис. 2.14,б) легко пов'язати з
діаграмою y2 додаванням
до останньої верхнього рядка одиниць: D27=y2+![]() , а діаграми K27 і y3 збігаються: K27=y3. Отже, з урахуванням D35=y2+x3 маємо
, а діаграми K27 і y3 збігаються: K27=y3. Отже, з урахуванням D35=y2+x3 маємо
![]()
тобто функція реалізується елементом АБО.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.