Логічні основи цифрової техніки (Глава 2 навчального посібника), страница 6

3. Перехід до досконалих форм від таблиці відповідності. Під час логічного проектування доводиться користуватися різними формами зображення функціонування ЦП: таблиці відповідності, вирази логічної функції того чи іншого типу, діаграми й ін. Ці форми щільно пов'язані між собою і можуть розглядатися як математичні моделі ЦП, бо віддзеркалюють різними мовами один і той самий зв'язок вихідного сигналу зі вхідними. Розглянемо способи  перетворення між поширеними формами зображення функцій.

Від словесного або іншого способу задання логічної функції досить легко перейти до формального її опису. Для цього необхідно: 1) з'ясувати, скільки     входів та виходів має пристрій, 2) встановити, які значення мають функції на кожному з виходів за всіх можливих сполучень вхідних змінних і 3) скласти таблицю відповідності або безпосередньо ДДНФ функції.

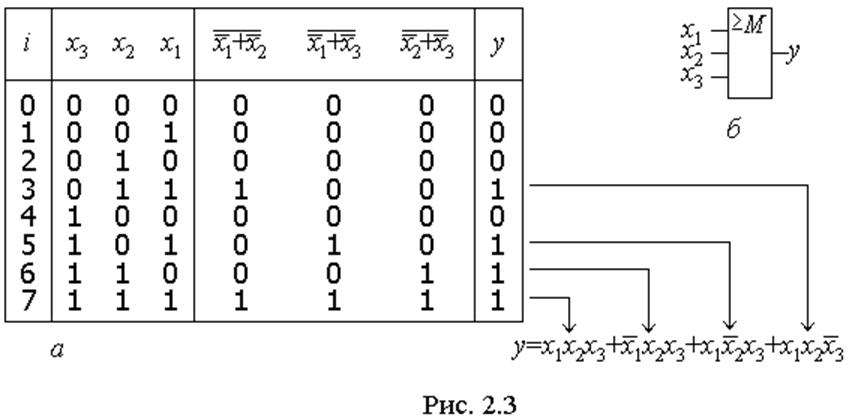
Припустимо, логічна функція задана словесно таким чином: на виході пристрою встановлюється рівень лог. 1, якщо не менш, ніж на двох із трьох його входів діють рівні лог. 1. За таким описом будуємо таблицю відповідності        (рис. 2.3,а), яка містить три змінні та одну функцію у, за одиничними значеннями якої безпосередньо з таблиці записуємо її ДДНФ (подано стрілками). Така функція реалізується мажоритарним елементом, загальне умовне позначення якого наведено на рис. 2.3,б (у прикладі М=2).Так само за нульовими значеннями функції легко перейти до її ДКНФ.

Якщо логічна функція задана виразом довільної форми, наприклад,

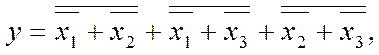
то для переходу до ДДНФ (або ДКНФ) спочатку можна скласти таблицю відповідності за методом прямої індукції (див. рис. 2.3,а): обчислюються логічні значення компонентів виразу для кожного кортежу, та, як підсумок, значення всієї функції у зводяться в колонку. Далі переходимо до ДДНФ як звичайно.

4. Аналітичний перехід до досконалих форм. За іншим способом від  вихідної формули переходимо до ДДНФ алгебрично:

а) позбуваючись інверсій над виразами (залишаючи їх,  у разі потреби, тільки над окремими змінними), переходимо за законом двоїстості до ДНФ, тобто в нашому прикладі маємо:

б) розгортаємо терми (компоненти) ДНФ таким чином, щоб кожний з них мі-стив усі змінні (за аксіомами х·1=х, 1=):

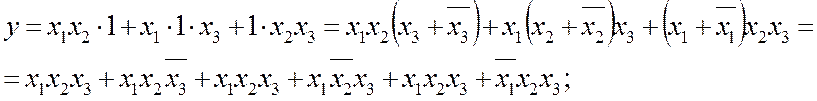
в) якщо виникають дублікації (повторення однакових термів), скорочуємо їх (за аксіомою: х+х=х) і здобуваємо остаточний вираз ДДНФ:

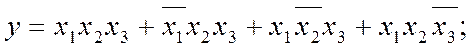
г) за необхідністю відтворюємо таблицю відповідності у зворотному порядку: заступаючи літерали в мінтермах їх цифровими значеннями (змінну з інверсією замінюємо нулем, а без інверсії – одиницею, наприклад, 0112=310=i), визначаємо коди i вхідних кортежів, що відповідають значенням у=1, а на інших  кортежах записуємо у=0.

Аналогічно перетворюємо функцію й до ДКНФ: спочатку позбуваємося інверсій над виразами і розгортаємо функцію до КНФ за розподільчим законом 8б (див. табл. 2.2):

у=х1х2+х1х3+х2х3=(х1+х1+х2)(х1+х1+х3)(х1+х3+х2)(х1+х3+х3)xx(х2+х1+х2)(х2+х1+х3)(х2+х3+х2)(х2+х3+х3)=(х1+х2+х3)(х1+х2)(х1+х3)(х2+х3).

Відтак доповнюємо кожну диз’юнкцію змінними, яких бракує для утворення досконалої форми (за аксіомами x+0=x, 0=):

По усуненні дублікацій типу x.x=x у розглядуваному прикладі дістанемо ДКНФ

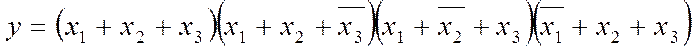
Зв’язок між ДКНФ і таблицею відповідності встановлюємо аналогічно як для ДДНФ: макстерми (вирази в дужках) визначають нульові набори функції, наприклад, 0012 =110 = i, а всі інші  набори відповідають значенню функції у=1.

Таким чином, якщо функціонування пристрою задано логічним виразом, то виконуємо перетворення в  загальному випадку за послідовністю: мішана форма – ДФ (КФ) – ДНФ (КНФ) – ДДНФ (ДКНФ). І, нарешті, від фунції в ДДНФ (ДКНФ) легко перейти до її інверсії відповідно в ДКНФ (ДДНФ) взаємною заміною прямих і інверсних змінних та знаків диз'юнкції і кон'юнкції згідно з (2.1).

2.1.5. Співвідношення між логічними функціями

Алгебра логіки ізоморфна (взаємно відповідає) алгебрі множин відносно операцій об'єднання (диз'юнкції), перетину (кон'юнкції) та доповнення (інверсії). Це уможливлює використання діаграм Венна (діаграм Ейлера) для наочної ілюстрації властивостей алгебри логіки й розв'язання логічних рівнянь за допомогою алгебри множин.