Непараметрическая идентификация линейных систем. Идентификация весовой функции по текущим наблюдениям

ГЛАВА 4.

 НЕПАРАМЕТРИЧЕСКАЯ ИДЕНТИФИКАЦИЯ ЛИНЕЙНЫХ  СИСТЕМ (ЛС)

4.1 Графо-аналитические методы

Методы данной группы являются простейшими в задачах типовой идентификации. К группе непараметрических методов их можно отнести условно, в том смысле, что в результате обработки данных и вычислений параметры временных и частотных характеристик частотных звеньев, имеющие ясный физический смысл на языке коэффициентов передачи и постоянных времени, а не сами эти характеристики, как решение некоторых уравнений идентификации.

Графические и графо-аналитические методы используются обычно при условиях, близких к лабораторным, когда объект можно возмущать специальными пробными сигналами (активная идентификация) и когда уровень помех измерений настолько мал, что ими можно пренебречь. Данные методы идентификации используются в основном для определения параметров простейших моделей. Рассмотрим некоторые из методов применительно к конкретным моделям.

1.  Статистический объект описывается уравнением

,                                  (4.1.1)

где  k– коэффициент усиления. Для его определения достаточно подать на вход объекта постоянный сигнал uD(t), где D(t) – единичная функция Хевисайда, и замерить выходной сигнал (рис.4.1.1), так как

 

рис.4.1.1.

 .                                      (4.1.2)

2.  Объект описывается уравнением идеального интегратора

                                            .                                    (4.1.3)

Реакция такого объекта на единичное ступенчатое входное воздействие при x(t)=0 показана на рис.4.1.2. Коэффициент k определяется как тангенс угла наклона прямой y(t):

                                                                   .                                        (4.1.4)

 

рис.4.1.2.

3.  Объект описывается уравнением первого порядка

                                                   ,                       (4.1.5)

где  Т – постоянная времени объекта,

k – коэффициент усиления.

При u(t)= u_OD(t) и y(t_O)=0 выходной сигнал объекта y(t) имеет вид экспоненты

, изображенной на рис.4.1.3. Очевидно, что

                                                                          (4.1.7)

Кроме того, для тангенса угла наклона касательной к экспоненте (4.1.6) в начале координат имеем

                                                                    (4.1.8)

Из треугольников ОАВ и ОСВ имеем

                                                         T=ОС=АВ .                        (4.1.9)

Нетрудно показать, что в момент времени t=ОС=Т величена выходного сигнала достигает значения

                                                         .                      (4.1.10)

Таким образом, при значительных t выражение (4.1.7) даёт возможность оценить коэффициент усиления k. После этого постоянная времени может быть найдена графически, как абсцисса точки G (см. рис.4.1.3).

Известно, что для оценки постоянной времени может быть использована касательная к экспоненте в любой её точке. Действительно, пусть к кривой y(t) касательная проведена в точке F, соответствующей моменту времени t₁. Построим прямоугольный треугольник FQQ₁ .

 

рис.4.1.3.

Для угла g имеем

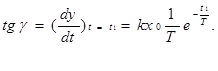
Тогда

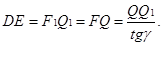
Длина отрезка

в результате DE=T. Следовательно, проекция отрезка любой касательной от её начала до пересечения с прямой y(t)=y_УСТ на ось абсцисс равна постоянной времени Т.

Указанная методика имеет недостаток, вызванный необходимостью доведения процесса до установившегося состояния, что требует, особенно при больших значениях Т, значительного времени.

 

рис.4.1.4.

Существуют методы, лишённые этого недостатка. Они позволяют находить коэффициент усиления и постоянную времени только по участку экспоненты y(t). Идея одного из методов заключается в следующем. Снимается часть выходного сигнала объекта при подаче на вход постоянного воздействия (рис.4.1.4). На основании кривой y(t) во втором квадранте строится график зависимости . Для этого можно воспользоваться одним из способов графического дифференцирования.  Пусть таким образом мы построим линию АВ.  Из уравнения (4.1.5) имеем

                                                         ,                       (4.1.11)