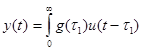Непараметрическая идентификация линейных систем. Идентификация весовой функции по текущим наблюдениям, страница 5

                                                                        (4.4.1)

                                         ,                                    (4.4.2)      где

, а R_u(t) и R_v(t) известные ковариационные функции,

- символ математического ожидания.

Умножая обе части (4.4.2) на u(t-t) и применяя операцию математического ожидания, получим

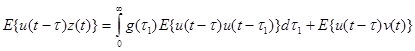             ,    (4.4.3)

или

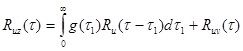                                    ,               (4.4.4)  где R(.) – соответствующие ковариационные функции. Если входной сигнал и сигнал помехи некоррелированы, то 

и получим основное уравнение идентификацииотносительно весовой функции g(t), известное как уравнение Винера-Хопфа

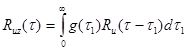                                                               (4.4.5)

Интегральное уравнение  (4.4.5) может быть получено из условия минимума по g(t) дисперсии ошибки выхода, т.е.

.

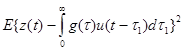Если входной сигнал является белым шумом, то

и решение задачи значительно упрощается. Из уравнения (4.4.5) непосредственно получаем

, откуда

                                                                              (4.4.6)

Структурная схема идентификации для этого частного случая приведена на рис.4.4.2.

 

В общем случае произвольного входного сигнала, решение задачи идентификации сводится к численному решению основного уравнения идентификации (4.4.5).

Рассмотрим способ решения этой задачи, основанный на конечно-разностной аппроксимации. Произведём “усечение” весовой функции идентифицируемого объекта, т.е. положим

рис.4.1.3.

при

t>t₁=nT, где n – число интервалов разбиения  на [0, t₁],

T – величена каждого интервала.

Тогда основное уравнение (4.4.5) примет вид

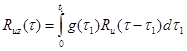                                                              (4.4.7)

применим ступенчатую аппроксимацию всех функций на интервале [0, t₁], т.е. положим

и

                                                                       (4.4.8)

Уравнение (4.4.7) в этом случае можно записать в точке t=kT следующим образом

                                            (4.4.9)

Подставляя в (4.4.9) последовательные значения k=(0,n), получим

:  

:  

……………………………………………………………………………         (4.4.10)

:  

Вводя в рассмотрение вектор-столбцы

,

размером “n+1” и квадратную симметричную матрицу

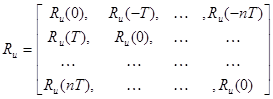
размером “(n+1)x(n+1)”,

линейную систему алгебраических уравнений записываем в виде

                                                 ,                               (4.4.11)

откуда при , т.е. при  имеем

                                                                                 (4.4.12)

Элементы матриц R_u и R_uz определяются путём вычисления оценок ковариационных функций по формулам

                                    ,                     (4.4.13)

и                                                                                                                          

Все вычисления, необходимые для получения решения (4.4.12) легко реализуются в среде MATLAB for Windows.

В заключении отметим, что обратные задачи теории управления, сводящиеся к решению основного уравнения идентификации (4.4.7) относятся к классу некорректных задач, в которых даже малые погрешности задания исходных данных приводят к неустойчивым  вычислительным схемам и, как следствие, к значительным искажениям получаемых решений. Основные пути преодоления указанных трудностей состоят в применении методов регуляризации некорректных задач.