Непараметрическая идентификация линейных систем. Идентификация весовой функции по текущим наблюдениям, страница 2

т.е. зависимость является линейной. Поэтому линия АВ есть прямая и может быть продолжена для пересечения с осями координат соответственно в точках С и D. Так как в точке D  , то из соотношения (4.1.11) следует:

, откуда

                                               ,                                      (4.1.12)

В точке С  y(t)=0, поэтому из выражения (4.1.11) получим

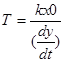                                                 ,                                    (4.1.13)

3.  Объект описывается уравнением колебательного звена

                                 ,                    (4.1.14)

где a₀ =1;

a₁ =2xw₀;

      a₂=w²₀;

          b₀= w²₀k ; 

 - коэффициент относительного затухания;

w₀ - частота свободных колебаний;

 k – коэффициент усиления.

График переходной функции колебательного звена изображён на рис.4.1.5. Аналитически переходная функция описывается выражением

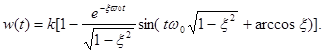                          (4.1.15)

Очевидно, что

                                                     ,                            (4.1.16)

т.е. коэффициент усиления определяется из графика как расстояние до асимптоты затухающего процесса.

Относительный коэффициент затухания определяется несколькими способами. Перечислим некоторые из них.

Для объекта, описываемого математической моделью (4.1.14), выражение весовой функции имеет вид

          .                           (4.1.17)

Выражение (4.1.17) может быть получено формально дифференцированием по t переходной функции (4.1.15). Сравнение функций (4.1.15) и (4.1.17) показывает, что они сдвинуты по фазе на угол j , связанный с коэффициентом соотношением

               ,                                  (4.1.18)

откуда

                                             .                                      (4.1.19)

Таким образом, для оценки коэффициента по формуле (4.1.19) необходимо замерить сдвиг фаз между кривыми h(t) и w(t). Отметим, что фазу j можно найти и без построения весовой функции. Для этого достаточно определить фазовый сдвиг гармонической составляющей

переходной функции относительно начала координат. На рис.4.1.5 гармоническая составляющая изображена пунктиром.

Весьма эффективно можно определить коэффициент затухания путём сравнения двух смежных амплитуд и площадей полуволн весовой функции h(t) или колебательной составляющей переходной функции w(t). Более помехозащищённым является  способ, основанный на сравнении площадей смежных полуволн. Так, для процесса h(t) площадь первой полуволны

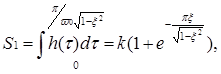
площадь второй полуволны

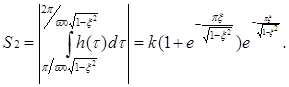
Логарифм отношения площадей

                                             (4.1.20)

Для малых (больших затуханий) имеем

                                                                       (4.1.21)

Для определения величены параметра w₀ необходимо непосредственно по кривой w(t) найти собственную круговую частоту колебаний w по формуле

Частота w связана с параметром w₀ соотношением

откуда при известном получим

В рассмотренных методах не учитывались случайные ошибки измерений. В принципе при наличии этих ошибок и помех все расчетные соотношения и формулы могут быть использованы в статистическом плане.

4.2 Идентификация весовой функции по текущим наблюдениям.

Уравнение вход-выход линейного объекта во временной области имеет вид:

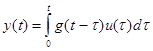                                                 (4.2.1)

где g(t) – весовая функция системы,

u(t) – входное воздействие.

Заменим входной сигнал u(t) его ступенчатой аппроксимацией, т. е. положим (рис.4.2.1)