Непараметрическая идентификация линейных систем. Идентификация весовой функции по текущим наблюдениям, страница 4

Приравнивая вещественные и мнимые части, получим

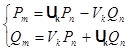                                                                          (4.3.4)

Если a_n=1, то

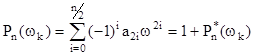
Разрешим уравнение (4.4.4) относительно U_k  и V_k :

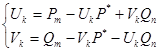                                                                     (4.3.5)

Введем обозначения :

  U=[U₁,U₂,...,U_n]^T  ,  V=[V₁,V₂,...,V_n]^T;

  T₁=diagU;  T₂=diagV;

        ;  a=     

     ;  a=

        ;  b=

       ;  b=

Система (4.3.5) записывается в векторно-матричной форме в следующем виде:

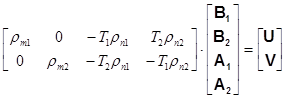                               ,            (4.3.6)

где  A₁=[a₀,a₂,...,a_n1]^T,

       A₂=[a₁,a₃,...,a_n2]^T ,

       B₁=[b₀,b₂,...,b_m1]^T ,

       B₂=[b₁,b₃,...,b_m2]^T .

Система (4.3.6) может быть переписана в виде

D×x = C ,

где D, x, C- матрицы соответствующих размеров. Решение системы  имеет вид

= D⁺C, или

=(D^T×D)^-1DTC , при соответствующих размерах матриц, где D⁺ - псевдообратная в смысле Мура- матрица; характеризуется следующими определяющими свойствами

НН⁺Н=Н,  Н⁺НН⁺=Н⁺.

Существует модификация метода:

Вводится невязка

                                               (4.3.7)

Задача идентификации сводится к минимизации величины . Умножим (4.3.7) на A(w_k):

                               A(w_k)e(w_k) = A(w_k)W(jw_k)-B(w_k)                (4.3.8)

Представим равенство (4.3.8) в алгебраической форме:

A(w_k)e(w_k)=P(w_k)+jQ(w_k)ÞçA(w_k)e(w_k)ï² = P²(w_k)+Q²(w_k)

Новая функция ошибок:

Имеем

B(w_k) = a + jwb ; A(w_k) = s + jwt ;

P(w_k) = Re{A(w_k)W(jw_k)-B(w_k)}= Re{[s_k + jw_kt_k](U(w_k)+jV(wk))-(a_k+jw_kb_k)}= s_kU_k - w_kt_kV_k - a_k ;

Аналогично

Q(w_k) = Im{...}= w_kt_kU_k + s_kV_k - w_kb_k

Таким образом имеем :

                   J=         (4.3.9)

a_k= b₀ - b₂ + b₄- ...

b_i = b₁ - b₃ + b₅- ...

s_i = 1 - a₂ + a₄- ...

t_i = a₁ - a₃ + a₅-...

Приравнивая градиент J к нулю, получим линейную систему алгебраических уравнений относительно неизвестных параметров:

, где  x = [b₀,b₁,...,b_n,a₁,a₂,...,a_n] вектор параметров системы,

- символ градиента.

Решение этой системы приводит к окончательному результату.

Недостаток метода заключается в том, что должен быть заранее известен порядок уравнений системы.

Рассмотрим частные случаи, отвечающие простейшим звеньям первого и второго порядков.

1. Система первого порядка:

 ;

Полагая

S = jw,

получим

= g + jb .

Откуда следует равенство

                              (4.3.10)

Приравнивая левые и правые части равенства(4.3.10), получим систему уравнений:

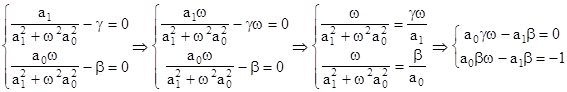
откуда

 ,  ;

Измерения A(w₁) и Q(w₁) дает g(w₁) = g₁и b(w₁) = b₁, откуда производят вычисление {a₀ ,a₁}

По значениям a₀  и a₁  определяются параметры исходной системы

и

 .

Можно рассмотреть вариант измерения амплитуд в точках w₁  и  w₂:

Решив систему получим:

  ;

 .

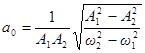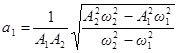2. Система второго порядка:

;

Для каждой частоты w_i можно определить два параметра, поэтому система уравнений доопределяется введением последовательно звена 1-го порядка:

Таким образом

, где с₀ = a₃T ,  c₁ = a₁T + a₀ ,  c₂ = a₂T + a₁ , c₃= a₂ .

Система уравнений примет вид:

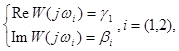
откуда

 

полагая  и  получим

  ,

  ,

  ,

 , где - главный определитель линейной системы.

4.4.  Корреляционный метод идентификации линейных систем

    Рассмотрим соотношение “вход-выход” стационарной непрерывной линейной системы с точкой приложения помехи к выходу (рис.4.4.1)

рис.4.4.1.