Информатика и выч. техника \ Моделирование систем и комплексов

Непараметрическая идентификация линейных систем. Идентификация весовой функции по текущим наблюдениям, страница 3

u(t)»u(kT) ,

при

kT £ t £ (k+1)T

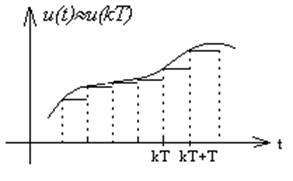
Рис. 4.2.1

Весовая функция принимается равной значению в середине интервала квантования (рис. 4.2.2).

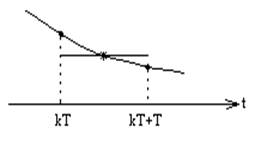
Рис.4.2.2

k T£ t < (k+1)T

Интеграл (4.2.1) после принятых аппроксимаций примет вид:

(4.2.2), где к=0,1,…

Вводим в рассмотрение вектор наблюдений:

y(T) = [y(T),y(2T),...,y(kT)]^T

- размером (кx1) и вектор весовой функции в точках квантования

- размером (кx1);

Положим в выражении (4.2.2) k = 0,1,2,... ,тогда последовательно будем иметь

;

; (4.2.3)

;

........................................................................................

Образуем матрицу входа:

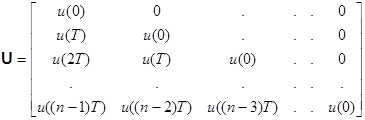- матрица размером n´n

Тогда основное уравнение вход-выход (4.2.2) можно записать в следующем виде :

, (4.2.4)

где êUê=[u(0)]ⁿ¹0, поэтому U^-1 существует.

Из выражения (4.2.3) получим :

, (4.2.5)

где =TU

Выражение (4.2.5) благодаря виду матрицы U можно переписать в рекуррентной форме :

, (4.2.6)

где и

Действительно из уравнений (4.2.3) имеем:

, откуда

Далее ,

и т.д.

В выражении (4.2.5) с ростом “k” растет объем вычислений, при этом для определения g(nT) нужно 2n умножений и сложений.

Для обеспечения адаптивной идентификации требуется высокое быстродействие. Этот недостаток является основным. Преимуществом данного подхода является возможность работы при пробных сигналах и на любых реализациях в режиме нормального функционирования.

Частный случай:

Если на входе системы единичное ступенчатое воздействие

U(iT)=1(iT),

то выражение (4.2.6) примет вид :

(4.2.7)

Определив имеем:

, где Q_k = Q_k-1+ g_k-1

Основные осложнения в обсуждаемом методе связаны с наличием помехи в измерении выхода. Главные пути преодоления трудности – воспроизведение, если возможно, одинаковых реализаций на входе с последующим усреднением результатов, и применение процедуры усечения весовой функции полагается:

g(nT)=0,

при n>k, и организуется продолжение наблюдений при n>k. Матрица входов U – (kxk) увеличивает количество строк, сохраняя количество столбцов. Начиная с “k+1” шага можно применять рекуррентный алгоритм метода наименьших квадратов (см. раздел 6.2).

4.3 Оценка параметров систем по частотным характеристикам.

Пусть W(S)- передаточная функция неизвестной системы

; (4.3.1)