Модели линейных объектов в задачах идентификации. Частные структуры линейных моделей с помехой

ГЛАВА 2

МОДЕЛИ ЛИНЕЙНЫХ ОБЪЕКТОВ В ЗАДАЧАХ ИДЕНТИФИКАЦИИ

2.1. Общая структура линейных моделей с помехой

Рассмотрим множество моделей линейных стационарных объектов с дискретным временем, с учетом неконтролируемых воздействий. Все неконтролируемые сигналы в этом случае принято сводить к аддитивной помехе, приложенной к выходному сигналу системы (Рис.2.1.1), то есть

Рис.2.1.1

                                     (2.1.1)

Здесь

G(q)=B(q)/A(q) - дискретная передаточная функция системы;

u(t) - входной сигнал;

v(t) - стационарная случайная последовательность помехи;

z(t) - выходной сигнал;

qx(t)=x(t+1) - оператор сдвига вперед;

t=0, 1, 2, ... - дискретное время.

Последовательность v(t) имеет дробно-рациональную спектральную плотность, поэтому может быть представлена дискретным белым шумом n(t) ~ с нулевым средним и дисперсией , проходящим через линейную стационарную систему с весовой функцией h(k):

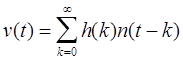                                   (2.1.2)

Из выражения (2.1.2) получим

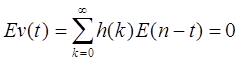, где Е - символ математического ожидания

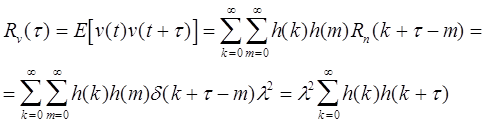(2.1.3)

ковариационная функция сигнала помехи, так как

, где - дискретная функция Дирака.

Вводя в рассмотрение оперативную передаточную функцию

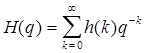                                        (2.1.4)

выражение (2.1.2) записывается в оперативной форме

                                                 (2.1.5)

где H(q)=C(q)/D(q) - операторная передаточная функция,

n(t) ~ - дискретный белый шум.

Применяя к обеим частям соотношения (2.1.3) z - преобразование, получим выражение для спектральной плотности помехи

                 (2.1.6)

Если белый шум n(t) имеет единичную интенсивность , то будем иметь

                    (2.1.7)

откуда следует, что для любой дробно-рациональной спектральной плотности  возможно единственное разложение (2.1.7), называемое факторизацией спектральной плотности: H(z) - передаточная функция формирующего фильтра, имеющее шум и полосы внутри единичного круга, т.е. отвечает устойчивой, минимально-фазовой системе.

С учетом выражения (2.1.5) соотношение “вход - выход” модели принимает вид:

                                  (2.1.8)

где G(q)=B(q)/A(q); H(q)=C(q)/D(q) - дискретные операторные передаточные функции по входу и помехе соответственно;

u~ - входная последовательность  с нулевым средним и ковариационной функцией .

n ~ - дискретный белый шум с нулевым средним и дисперсией .

Структурная схема отвечающая (2.1.8) изображена на рис.2.1.2.

Рис.2.1.2

2.2  Частные структуры линейных моделей с помехой

Пусть в выражении (2.1.8)

;

, тогда можно записать уравнение объекта в операторной форме

                               (2.2.1)

где A(q)=1+a₁q^-1+...+a_nq^-n - характеристический многочлен;

B(q)=b₁q^-1+...+b_mq^-m - многочлен по входному воздействию;

C(q)=c₀+c₁q^-1+...+c_pq^-p - многочлен по возмущению (помехе).

Структурное представление (2.2.1) изображено на рис.2.2.1.

Рис.2.2.1

Модель, описываемая уравнением (2.2.1), называется моделью авторегрессии скользящего среднего (АРСС).

Рассмотрим частные случаи моделей, отличающиеся характером формирования сигнала помехи V(t).

1. Модель ошибки уравнения

Положим в уравнении C(q)=1, тогда

и уравнение (2.2.1) принимает вид

                                      (2.2.2)

или в развернутом виде

 (2.2.3)

Уравнение (2.2.3) является одним из самых простых и доступных для практических исследований, так как белый шум n(t) выходит в (2.2.2) как непосредственная ошибка уравнения

, то модель (2.2.2) называют моделью ошибки уравнения.

Структура модели изображена на рис.2.2.2

.

Рис.2.2.2

2. Модель выходной ошибки