Модели линейных объектов в задачах идентификации. Частные структуры линейных моделей с помехой, страница 2

Соответствует случаю приложения помехи n(t) к выходу объекта (Рис.2.2.3).

Рис.2.2.3

В этом случае уравнение объекта принимает вид:

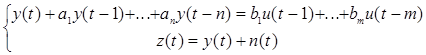
Откуда непосредственно записывается уравнение относительно выхода

                                                                                                                               (2.2.4)               

3. Модель авторегрессии (АР-модель)

Получаются из общего уравнения (2.2.1), если положить

,

                                               (2.2.5)

или

                       (2.2.6)

Рис.2.6

4. Модель скользящего среднего (СС-модель) или регрессионная.

Полагая в (2.2.1)

,

C(q)=1,

Получим

,

(Рис.2.1.7)

и следовательно

                                      (2.2.7)

               (2.2.8)

Рис.2.2.5

Уравнение (2.2.8) соответствует как динамическому объекту с конечным временем переходного процесса, так и многомерному статическому объекту (Рис.2.2.6)

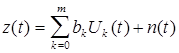                                   (2.2.9)

Рис.2.8

2.3  Описание линейных объектов в виде линейной регрессии

Уравнение вход-выход (2.1.7) в отсутствие помехи принимает вид:

(2.3.1)

Введем в рассмотрение вектор  параметров объекта

и регрессионный вектор, составленный из входной и выходной последовательностей

Тогда уравнение (2.3.1) можно переписать в следующем виде

                                    (2.3.1)

Выражение (2.3.1) известно в прикладной статистике как линейная регрессия.

2.4  Модели синтезаторов динамических характеристик линейных объектов

При отсутствии априорных данных о математической модели линейного идентифицируемого объекта, приходится использовать аппроксимацию динамических характеристик. Модель объекта в общей схеме идентификации (Рис.1.6) строится в этом случае, в виде синтезатора динамических характеристик, который представляет собой систему ортогональных функций, по которой раскладывается неизвестная весовая функция. Функции ортогональной системы реализуются в виде совокупности линейных фильтров. В итоге синтезаторы состоят из динамических элементов (фильтров) с весовыми функциями  и настраиваемых коэффициентов .

Структура синтезаторов может быть параллельной (Рис.2.4.1) и последовательной (Рис.2.4.2).

Рис.2.4.1

Рис.2.4.2

Передаточная функция синтезатора параллельной структуры равна

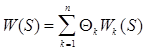,                                       (2.4.1)

где  - передаточные функции фильтров

Для синтезаторов параллельной структуры имеем

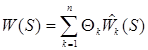, где

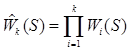                                      (2.4.2)

Часто используются синтезаторы на функциях Лагерра: полиномы Лагерра определяются в виде

и ортогоналы с весом

.

Если ортогонализовать полиномы Лагерра с весом

, то получим функции Лагерра, преобразование по Лапласу которых имеет вид, особенно удобный в реализации:

                                      (2.4.3)

Синтезатор Лагерра последовательной структуры изображен на рис.2.4.3.

Рис.2.4.3