|
||||||||
|
||||||||
|
||||||||
|
||||||||

Решение:
Входные параметры:
ξ= 280
n = 1000
Выходные параметры: Теоретический расчет:
μ = 30.853 μ = 31.100
σ = 112.564 σ = 112.570
Доверительный интервал:
[30.20, 31.51]
Оценка корреляционной функции:
j, ρ( j))
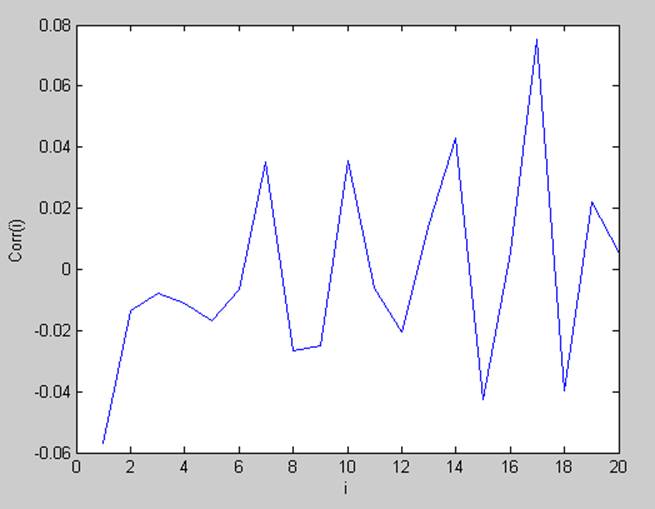
( Xj, Xj + 1 )
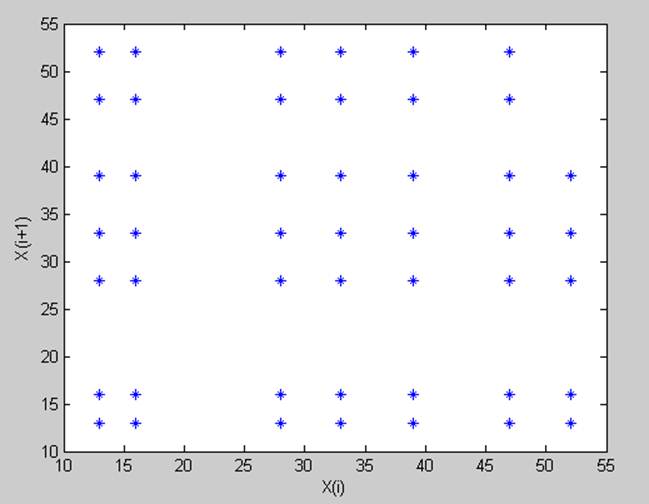
График частоты:
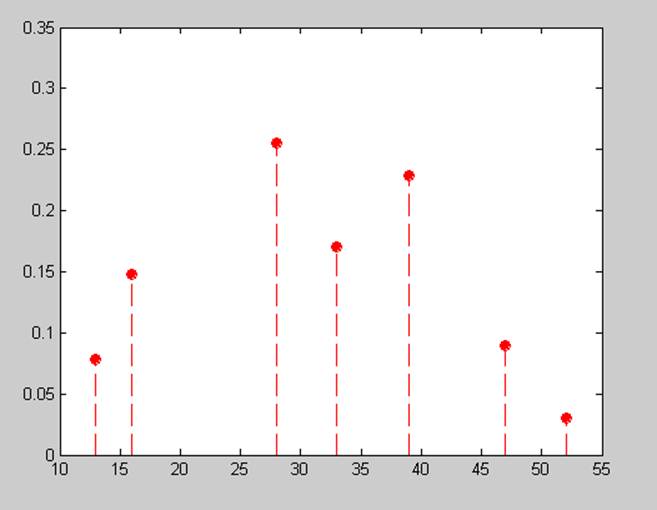
Судя по графику корреляции можно сделать вывод, что данная последовательность имеет случайную закономерность появления значений.
График зависимости последующей величины от предыдущей показывает, что все значения последовательности распределены между определенным набором значений Хi.
Полученные данные принимают одно из семи заданных значений.
Вследствие того что для формирования последовательности использовалось стандартное распределение, то последний график наглядно показывает что более длинным интервалам соответствует большее количество попаданий случайных величин гамма.
Максимальная частота появления в эксперименте x = 28. Вероятность p = 0.255
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.