Министерство общего и профессионального образования
Российской Федерации
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ, МЕХАНИКИ И ОПТИКИ
ОТЧЁТ
ПО ЛАБОРАТОРНОЙ РАБОТЕ №4
МАРКОВСКИЕ ПРОЦЕССЫ
Исполнитель,
студент группы 3715 _____________ О.А Борков
подпись, дата
Преподаватель _____________ Д.Г. Николаев
подпись, дата
Санкт-Петербург 2008
РЕФЕРАТ
В отчете 18 с., 15 рис., 1 прил.
ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №4 «МАРКОВСКИЕ ПРОЦЕССЫ»
Объектом исследования работы является моделирование дискретного марковского пространства.
Цель работы заключается в ознакомлении с марковскими сетями и разработке программы экспериментальных исследований дискретной цепи Маркова по следующему заданию:
Разработайте программу экспериментальных исследований дискретной цепи Маркова с матрицей переходных вероятностей:
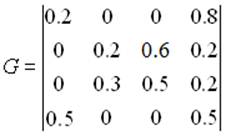
Рис 1.
Осуществите прогоны модели с начальными значениями, соответствующими состояниям цепи. Выведите на экран диаграммы изменения состояния системы, а также информацию о классах эквивалентных состояний системы, возвратных, нулевых и периодических состояниях, стационарное распределение вероятностей марковской цепи.
ВВЕДЕНИЕ
Марковский процесс, важный специальный вид случайных процессов, имеющих большое значение в приложениях теории вероятностей к различным разделам естествознания и техники.
Це́пь Ма́ркова — последовательность случайных событий с конечным или счётным бесконечным числом исходов, характеризующаяся тем свойством, что, говоря нестрого, при фиксированном настоящем будущее независимо от прошлого.
Последовательность дискретных случайных величин {Xn}n>=0 называется цепью Маркова (с дискретным временем), если
P(Xn+1=in+1 | Xn = in, Xn-1 = in-1, …, X0 = i0) = P(Xn+1=in+1 | Xn = in).
Таким образом, в простейшем случае условное распределение последующего состояния цепи Маркова зависит только от текущего состояния и не зависит от всех предыдущих состояний (в отличие от цепей Маркова высших порядков).
Область значений случайных величин {Xn} называется
простра́нством состоя́ний цепи, а номер n — номером шага.
ОСНОВНАЯ ЧАСТЬ
1. Суть метода генерации непрерывных случайных величин основывается на модели линейного конгруэнтного генератора равновероятной последовательности, в основе которого лежит зависимость следующего элемента последовательности от предыдущего, описываемая формулой:
xi+1 = (а*x i + с) mod m, (1)
где a, c, m - целые положительные константы.
Допустим, нам необходимо смоделировать дискретную цепь Маркова с матрицей переходных вероятностей. Для этого мы мы сгенерируем последовательность равной вероятности с помощью линейного конгруэнтного генератора. После чего, определяем начальное состояние X0 из условия:
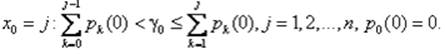
Затем на основе сгенерированной последвовательности создается последовательность состояний марковской цепи {xi}
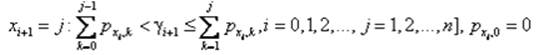
|
В данном практикуме требуется разработать программу экспериментальных исследований дискретной цепи Маркова с матрицей переходных вероятностей:
Рис. 2 |
В качестве значений параметров генератора Леммера выберем значения: a = 101, c=3, m=65536, X(1)=123, Y(1)=324.После чего производится деление всех элементов непрерывных последовательности на коэффициент m и домножение на коэффициент 65536, чтобы полученные последовательности находились в интервале от 0 до 1. Затем на основе чисел генерируется последовательность дискретных величин заданного распределения.
В системе MatLab это можно реализовать так:
%матрица переходных вероятностей
G = [[0.2 0 0 0.8 ]
[0 0.2 0.6 0.2 ]
[0 0.3 0.5 0.2 ]
[0.5 0 0 0.5 ]];
%длина последовательности генерируемых состояний
n=100;
%генерация массивов работы системы с разными условиями
S11=StateDim(1,n,1,G);
S12=StateDim(1,n,5,G);
S13=StateDim(1,n,10,G);
S1=SumMas(S11,S12,S13,n);
S21=StateDim(2,n,1,G);
S22=StateDim(2,n,5,G);
S23=StateDim(2,n,10,G);
S2=SumMas(S11,S12,S13,n);
S31=StateDim(3,n,1,G);
S32=StateDim(3,n,5,G);
S33=StateDim(3,n,10,G);
S3=SumMas(S11,S12,S13,n);
S41=StateDim(4,n,1,G);
S42=StateDim(4,n,5,G);
S43=StateDim(4,n,10,G);
S4=SumMas(S11,S12,S13,n);
%вывод на дисплей графиков
figure(1);
stairs(S11);
axis([0 100 0 5]);
figure(2);
stairs(S12);
axis([0 100 0 5]);
figure(3);
stairs(S13);
axis([0 100 0 5]);
figure(4);
stairs(S21);
axis([0 100 0 5]);
figure(5);
stairs(S22);
axis([0 100 0 5]);
figure(6);
stairs(S23);
axis([0 100 0 5]);
figure(7);
stairs(S31);
axis([0 100 0 5]);
figure(8);
stairs(S32);
axis([0 100 0 5]);
figure(9);
stairs(S33);
axis([0 100 0 5]);
figure(10);
stairs(S41);
axis([0 100 0 5]);
figure(11);
stairs(S42);
axis([0 100 0 5]);
figure(13);
stairs(S43);
axis([0 100 0 5]);
%вывод гистограмм
h=1:4;
figure(14);
hist(S1,h);
figure(15);
hist(S2,h);
figure(16);
hist(S3,h);
figure(17);
hist(S4,h);
function [x] = StateDim(x_beg,n,a_beg,G);
x_cur = x_beg;
x(1) = x_beg;
gamma_tmp=a_beg;
for i = 2:n,
x_tmp = 1;
p_tmp = G(x_cur, x_tmp);
gamma_tmp = mod (101 * gamma_tmp + 3, 65536);
gamma=gamma_tmp/65536;
while gamma > p_tmp;
x_tmp = x_tmp+1;
p_tmp = p_tmp + G(x_cur, x_tmp);
end;
x(i) = x_tmp;
x_cur = x_tmp;
end;
end
function [mass] = SumMas(x1,x2,x3,n);
for i=1:n,
mass(i)=x1(i);
mass(n+1)=x2(i);
mass(2*n+i)=x3(i);
end;
end
Диаграммы изменения состояния системы приведеня на рис.3 – рис.14. По три диаграммы с различными значениями для генератора изменения состояния системы на каждое из начальных значениях 1,2,3,4.
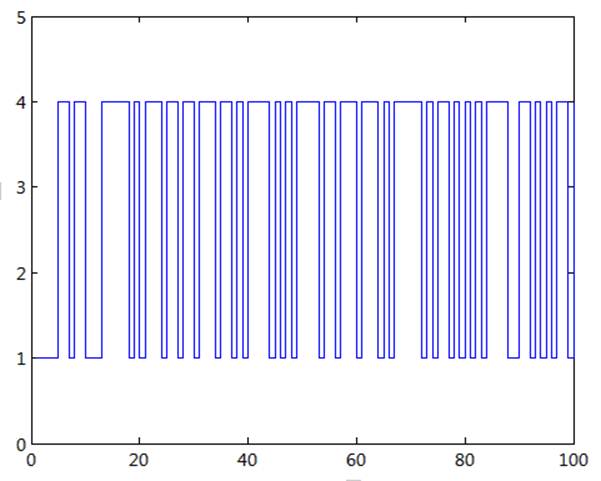
Рис 3. Диаграмма изменения состояния системы при начальном значении 1(1).
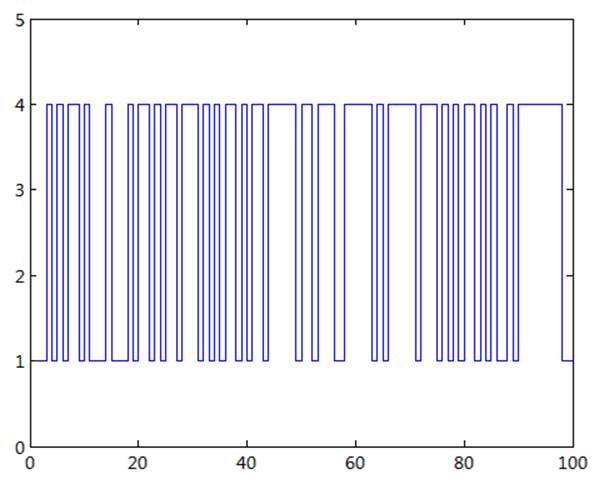
Рис 4. Диаграмма изменения состояния системы при начальном значении 1(5).
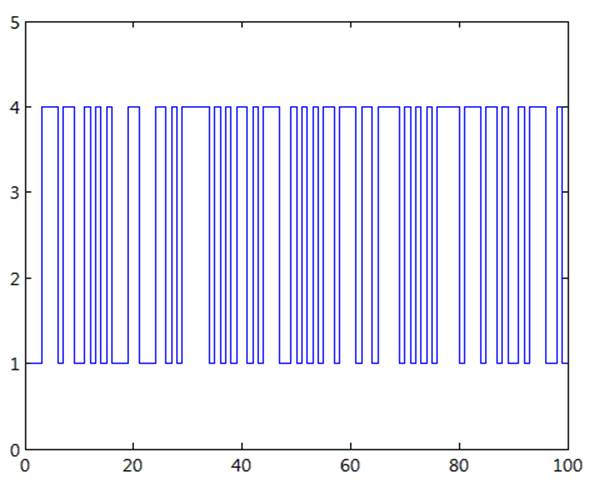
Рис 5. Диаграмма изменения состояния системы при начальном значении 1(10).
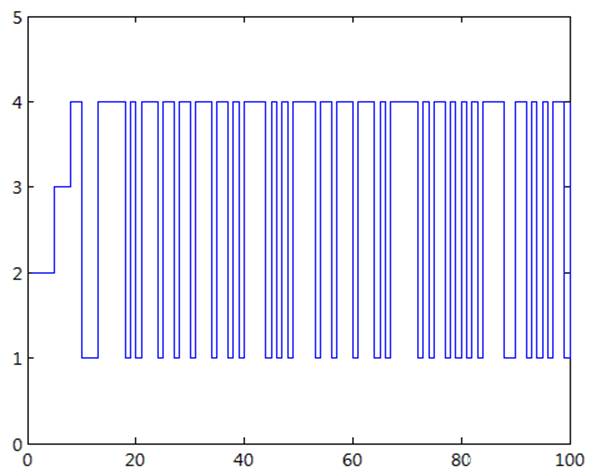
Рис 6. Диаграмма изменения состояния системы при начальном значении 2(1).
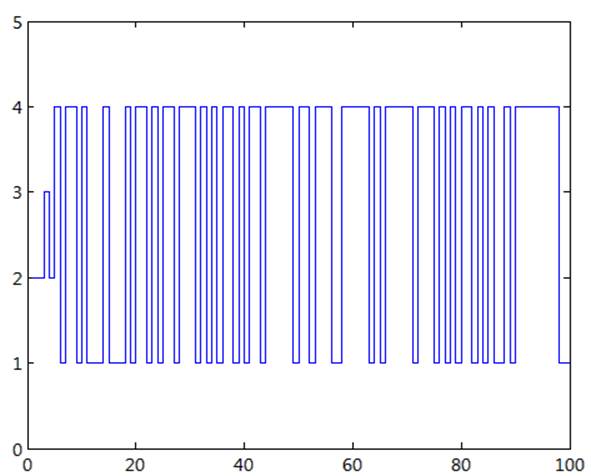
Рис 7. Диаграмма изменения состояния системы при начальном значении 2(5).
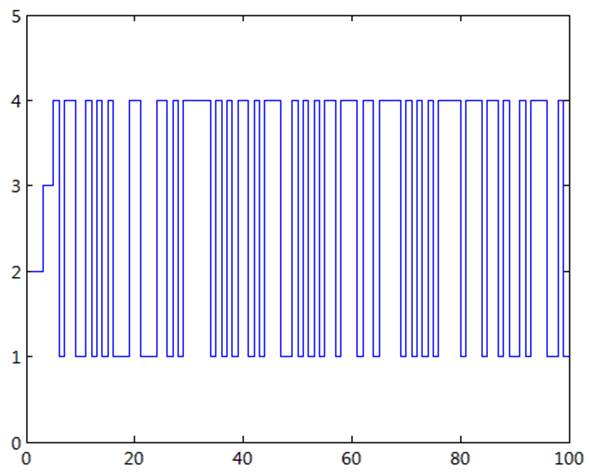
Рис 8. Диаграмма изменения состояния системы при начальном значении 2(10).
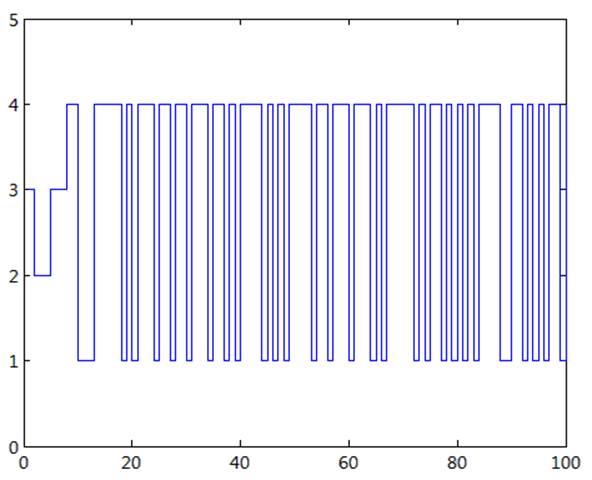
Рис 9. Диаграмма изменения состояния системы при начальном значении 3(1).
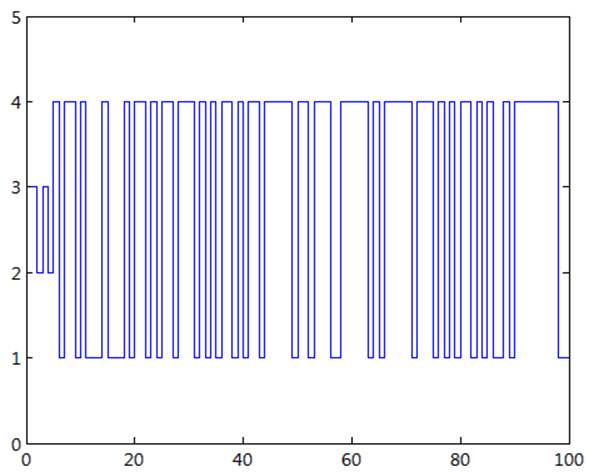
Рис 10. Диаграмма изменения состояния системы при начальном значении 3(5).
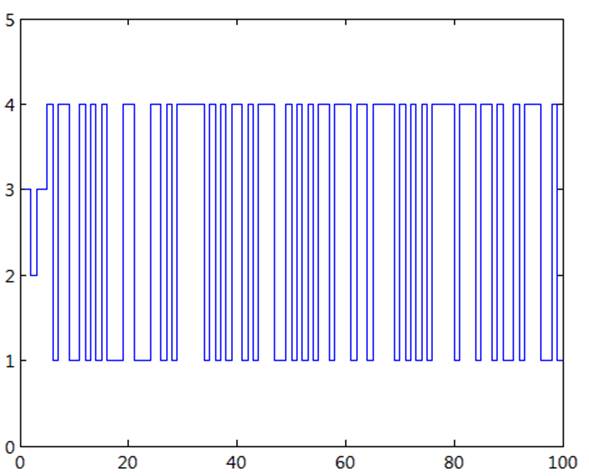
Рис 11. Диаграмма изменения состояния системы при начальном значении 3(10).
Рис 12. Диаграмма изменения состояния системы при начальном значении 4(1).
Рис 13. Диаграмма изменения состояния системы при начальном значении 4(5).
Рис 13. Диаграмма изменения состояния системы при начальном значении 4(10).
Поскольку число экспериментов в нашем случае очень большое, то при любых начальных состояниях можно наблюдать данную гистограмму распределения по состояниям:
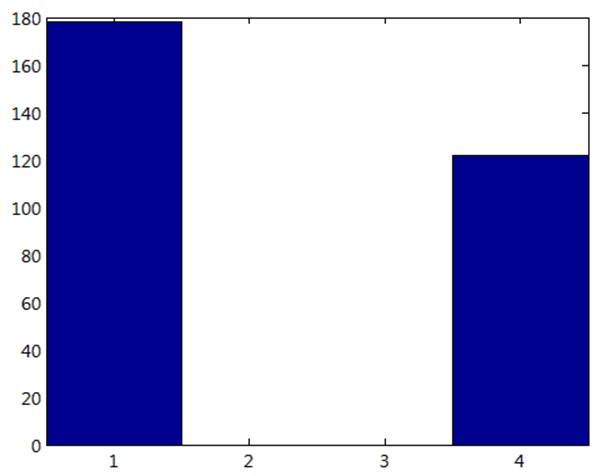
Рис.14. Гистограмма распределения по состояниям.
В нашем случае состояния 1 и 4 являются существенными, возвратными, ненулевыми, класс эквивалентности равен 1. Состояния 2 и 3 – нулевые, несущественные
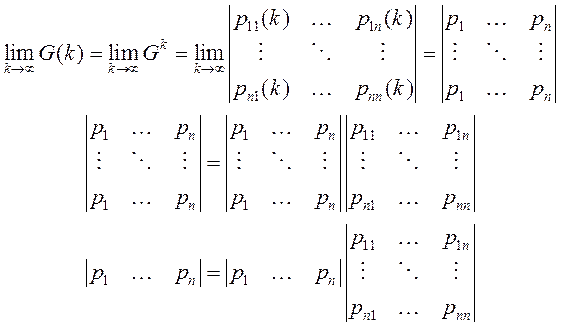 Условие стационарного распределения:
Условие стационарного распределения:
Решая систему уравнений в нашем случае получаем P = |0,384615 0 0 0,615385|
ЗАКЛЮЧЕНИЕ
Задание марковской цепи с помощью матрицы перехода за один шаг позволяет легко и наглядно анализировать систему, не прибегая к математическому анализу.
ПРИЛОЖЕНИЕ 1
Ниже приведён листинг кода на языке MatLab 7.0, реализующего программу экспериментальных исследований, содержащую в себе решение поставленных задач:
%матрица переходных вероятностей
G = [[0.2 0 0 0.8 ]
[0 0.2 0.6 0.2 ]
[0 0.3 0.5 0.2 ]
[0.5 0 0 0.5 ]];
%длина последовательности генерируемых состояний
n=100;
%генерация массивов работы системы с разными условиями
S11=StateDim(1,n,1,G);
S12=StateDim(1,n,5,G);
S13=StateDim(1,n,10,G);
S1=SumMas(S11,S12,S13,n);
S21=StateDim(2,n,1,G);
S22=StateDim(2,n,5,G);
S23=StateDim(2,n,10,G);
S2=SumMas(S11,S12,S13,n);
S31=StateDim(3,n,1,G);
S32=StateDim(3,n,5,G);
S33=StateDim(3,n,10,G);
S3=SumMas(S11,S12,S13,n);
S41=StateDim(4,n,1,G);
S42=StateDim(4,n,5,G);
S43=StateDim(4,n,10,G);
S4=SumMas(S11,S12,S13,n);
%вывод на дисплей графиков
figure(1);
stairs(S11);
axis([0 100 0 5]);
figure(2);
stairs(S12);
axis([0 100 0 5]);
figure(3);
stairs(S13);
axis([0 100 0 5]);
figure(4);
stairs(S21);
axis([0 100 0 5]);
figure(5);
stairs(S22);
axis([0 100 0 5]);
figure(6);
stairs(S23);
axis([0 100 0 5]);
figure(7);
stairs(S31);
axis([0 100 0 5]);
figure(8);
stairs(S32);
axis([0 100 0 5]);
figure(9);
stairs(S33);
axis([0 100 0 5]);
figure(10);
stairs(S41);
axis([0 100 0 5]);
figure(11);
stairs(S42);
axis([0 100 0 5]);
figure(13);
stairs(S43);
axis([0 100 0 5]);
%вывод гистограмм
h=1:4;
figure(14);
hist(S1,h);
figure(15);
hist(S2,h);
figure(16);
hist(S3,h);
figure(17);
hist(S4,h);
function [x] = StateDim(x_beg,n,a_beg,G);
x_cur = x_beg;
x(1) = x_beg;
gamma_tmp=a_beg;
for i = 2:n,
x_tmp = 1;
p_tmp = G(x_cur, x_tmp);
gamma_tmp = mod (101 * gamma_tmp + 3, 65536);
gamma=gamma_tmp/65536;
while gamma > p_tmp;
x_tmp = x_tmp+1;
p_tmp = p_tmp + G(x_cur, x_tmp);
end;
x(i) = x_tmp;
x_cur = x_tmp;
end;
end
function [mass] = SumMas(x1,x2,x3,n);
for i=1:n,
mass(i)=x1(i);
mass(n+1)=x2(i);
mass(2*n+i)=x3(i);
end;
end
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.