Задание

Анализ задачи и обзор аналогов
Пусть моделируемой системой будет телефонная станция, соединяющая абонентов. Дисциплина обслуживания: First In – First Out, т.е. абоненты обслуживаются в порядке живой очереди. Таким образом, требование, поступившее первым на устройство, обслуживается в первую очередь. Если при поступлении требования устройство занято, то вновь прибывшая заявка становится в очередь и обслуживается после того, как будут обслужены заявки, стоящие перед ней. Заявки на обслуживание поступают через случайные интервалы времени. Устройства служат для обслуживания этих заявок. Обслуживание длится некоторое случайное время. Если в момент поступления заявки все устройства заняты, заявка помещается в очередь и ждет начала обслуживания. По исходным данным имеется 2 телефонные линии, суммарная емкость: 48 абонентов. Среднее время поступления и обработки требований: 0.8 секунд.
При моделировании данной системы необходимо учесть минимальное и максимальное количество абонентов, стоящих в очереди на каждой линии, чтобы избежать простоя или, наоборот, переполнения количества заявок на телефонной станции.
Схема СМО
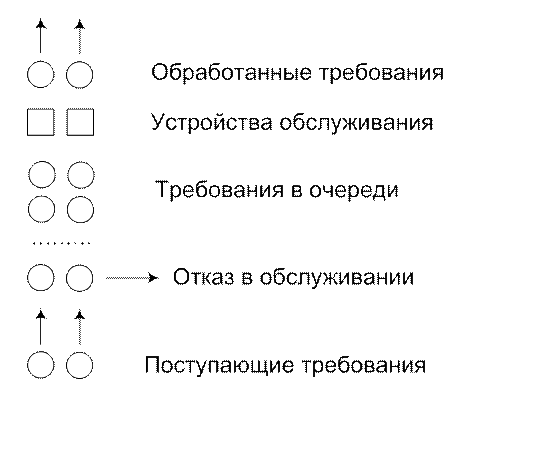
В моделируемой системе интервалы времени между поступлением требований являются независимыми случайными величинами со средним значением 0.8 с. Время обслуживания является также случайной величиной, некоррелированной с интервалами поступления требований. Среднее значение времени обслуживания требований – 0.8 с. Данные случайные величины являются непрерывными. Заявки поступают произвольно, т.е. без учета уже пришедших. Поэтому для данной случайной величины (время поступления заявки) следует выбрать экспоненциальное распределение. Такое же распределение выберем и для другой случайной величины – времени обслуживания заявки.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.