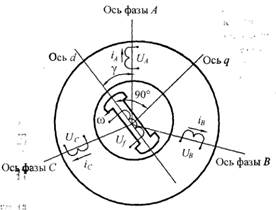
Рис. 1.1. Трехфазная симметричная модель синхронной машины
Предположим, что обмотки статора расположены симметрично как относительно друг друга, так и относительно осей вращения. Тогда магнитные оси трех фаз статора сдвинуты друг относительно друга на 120 электрических градусов. Если пренебречь потерями в стали и не учитывать насыщения во всех частях машины, то мгновенное значение напряжения на выводах любой из ее обмоток можно записать в виде
![]() (1.1)
(1.1)
где r - активное сопротивление обмотки;
i- ток;
![]() - результирующее
потокосцепление обмотки;
- результирующее
потокосцепление обмотки;
![]() - ЭДС индуктируемая в
обмотке.
- ЭДС индуктируемая в
обмотке.
Таким образом, для каждой обмотки приложенное к ней внешнее напряжение, за вычетом активного падения в обмотке, уравновешивается обратной ЭДС. Поскольку рассматриваемые четыре электрические цепи машины (три статорные обмотки и обмотка возбуждения) являются индуктивно связанными, то результирующее потокосцепление любой обмотки зависит от собственной индуктивности обмотки, взаимных индуктивностей между нею и другими обмотками и токов, протекающих в обмотках:
![]() (1.2)
(1.2)
где ![]() - собственная и взаимная
индуктивность цепей.
- собственная и взаимная
индуктивность цепей.
Обозначим параметры машины, относящиеся к ее статорным обмоткам, индексами А, В и С, а к обмотке возбуждения – индексом f. Рассмотрим генераторный режим синхронной машины, когда токи статора имеют направление от зажимов в сеть, а токи ротора, наоборот, имеют направление из сети к зажимам. Тогда с учетом направления токов и на основании (1.1) и (1.2) запишем уравнения для каждой из обмоток рассматриваемой синхронной машины:
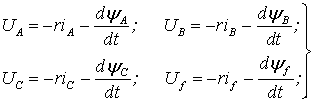 (1.3)
(1.3)
![]() (1.4,
а)
(1.4,
а)
![]() (1.4,
б)
(1.4,
б)
![]() (1.4,
в)
(1.4,
в)
![]() (1.4,
г)
(1.4,
г)
где r- активное сопротивление каждой фазной обмотки статора;
rf - активное сопротивление обмотки возбуждения;
LAA,…,Lff - собственные индуктивности обмоток;
LAB,…,LCf - взаимные индуктивности соответствующих обмоток.
Полученные уравнения (1.3 и 1.4) показывают взаимосвязь между напряжениями, токами, потокосцеплениями и позволяют полностью охарактеризовать переходный процесс в электрических цепях синхронной машины. Однако при исследовании электромагнитных и электромеханических переходных процессов электрическую машину целесообразно рассматривать как электродинамическую систему, состоящую из электрических цепей (обмоток) и вращающейся части (ротора). Необходимость такого рассмотрения синхронной машины объясняется взаимным влиянием электрических процессов и скорости движения ротора. Поэтому для описания поведения синхронной машины в переходном процессе систему уравнений (1.3-1.4) необходимо дополнить уравнением движения ротора
![]() (1.5)
(1.5)
где Мм - момент механических сил, приложенный со стороны вала машины;
МЭ - электромагнитный момент машины.
При работе машины генератором Мм является моментом первичного двигателя (турбины). При работе машины в режиме двигателя Мм представляет собой момент механической силы рабочего механизма, приводимого в движение двигателем. Момент МЭ в генераторе является тормозящим, в двигателе - движущим.
В установившемся режиме разностьМм – МЭравна нулю и изменение скорости вращения ротора не происходит. Однако при
возмущениях разность Мм – МЭ = ![]() не равна нулю, и ротор
электрической машины ускоряется или тормозится в зависимости от того, является
ли небаланс моментов
не равна нулю, и ротор
электрической машины ускоряется или тормозится в зависимости от того, является
ли небаланс моментов ![]() положительным или
отрицательным.
положительным или
отрицательным.
Индуктивности синхронной машины.Собственнаяиндуктивность обмотки ротора Lffне зависит от положения ротора в пространстве, так как по отношению к ней конфигурация магнитной системы остается неизменной при любом положении ротора и поэтому она имеет постоянное значение. Другие индуктивности, входящие в уравнения (1.4), изменяются во времени при вращении ротора. Индуктивность зависит от положения ротора вследствие того, что магнитная проводимость зазора для полей, создаваемых токами обмоток, из-за явнополюсности ротора зависит от его положения. Поэтому для решения дифференциальных уравнений (1.3) необходимо знать законы изменения индуктивностей в зависимости от положения ротора.
Условимся
положение ротора в пространстве определять углом у, на который продольная ось
опережает при вращении магнитную ось фазы А статора (см. рис.
1.1). При вращении ротора за время dtугол ![]() изменится на величину
изменится на величину ![]() .К произвольному времени t угол у определяется из
выражения
.К произвольному времени t угол у определяется из
выражения
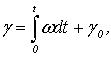 (1.6)
(1.6)
где
![]() - начальное значение угла
- начальное значение угла ![]() при t = 0.
при t = 0.
Если
угловая частота вращения ротора ![]() постоянна (
постоянна (![]() ), то угол
), то угол ![]() изменяется во времени по
закону
изменяется во времени по
закону
![]() (1.7)
(1.7)
Поскольку ротор периодически занимает одно и то же положение в пространстве, то очевидно, что и зависимость индуктивностей от угла будет периодической.
Собственная
индуктивность фазной обмотки статора всегда положительна и является
периодической функцией упга между магнитной осью фазы и продольной осью ротора
d. Поскольку изменение магнитных
потоков происходит гармонически с периодом ![]() , а не
, а не ![]() , так как при повороте ротора
на
, так как при повороте ротора
на ![]() повторяется цикл изменения
магнитного сопротивления, то зависимость собственной индуктивности фазы
статора от угла
повторяется цикл изменения
магнитного сопротивления, то зависимость собственной индуктивности фазы
статора от угла ![]() может быть выражена
уравнением
может быть выражена
уравнением
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.