Трехфазная симметричная модель синхронной машины. Математическая модель синхронной машины по Парку-Гореву, страница 4

Выразив токи  и  в (1.14) через токи  с помощью (1.13), получим для них ранее записанные выражения (1.12). Решая систему уравнений (1.12) относительно  получим формулы определения фазных токов машины при известных токах  и :

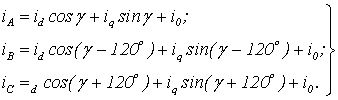                          (1.15)

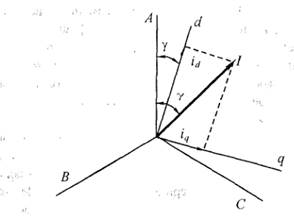
Рис. 1.5. Представление продольного и поперечного токов  с помощью изображающего вектора

Геометрический смысл преобразований (1.15) легко установить из диаграммы рис. 1.6.

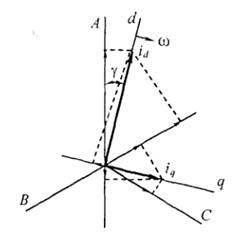
Рис.1.6. Определение мгновенных фазных токов через продольный и поперечный токи

Таким образом, в результате преобразования (1.12) можно вместо фазных токов , заданных любыми функциями времени, рассматривать токи  и . Удобство такого перехода заключается в том, что новые токи  и  в установившемся режиме имеют постоянные значения. Действительно, поскольку в установившемся режиме скорость вращения ротора и вектора  одинакова, то угол () не меняется (см. рис. 1.5). А если () = const, то согласно уравнению (1.14) и токи статора  и в системе координат, вращающейся вместе с ротором, являются величинами постоянными.

Поясним это: иногда образно говорят, что если бы исследователь, находящийся на роторе и вращающийся вместе с ним, наблюдал процесс изменения режимных параметров в статоре, то он видел бы их значения неизменными. И наоборот, если бы в фазе статора протекал постоянный ток, то исследователь на роторе наблюдал бы гармоническое изменение величин тока.

Следует отметить, что замену действительных фазных токов фиктивными токами  и , определяемыми по формулам (1.12), нельзя рассматривать только лишь как математические преобразования. В действительности новым токам можно дать физическое обоснование. Так величину   можно физически представить как мгновенное значение тока в фиктивной обмотке статора, вращающейся со скоростью ротора, ось которой в любой момент времени совпадает с продольной осью ротора. Значение тока в этой обмотке таково, что он создает такую же намагничивающуюся силу по продольной оси, как три действительных фазных тока, протекающих в реальных обмотках статора. Физическое истолкование тока  совершенно аналогично . Необходимо лишь помнить, что  действует не в продольной, а в поперечной оси.

Переход от действительных режимных параметров синхронной машины к переменным в осях d, q может быть выполнен не только для токов, но и для других величин. Замена, например, в (1.12) переменных;  на  или дает соответствующие уравнения преобразования для потокосцеплений или напряжений по осям dи q:

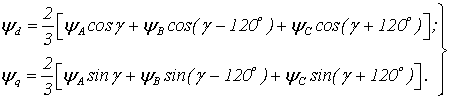            (1.16)

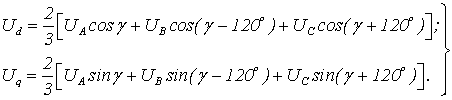           (1.17)

Таким образом, переход от трех исходных осей (А, В, С) к двум (dиq) физически означает замену рассматриваемой трехфазной машины эквивалентной двухфазной, в которой магнитные оси фазных обмоток сдвинуты на 90° электрических и вращаются вместе с ротором. На рис. 1.7 схематично изображены обмотки преобразованной синхронной машины.

Рис. 1.7. Упрощенная модель синхронной машины по Парку - Гореву

1.1.2.1.  Потокосцепления и сопротивления обмоток синхронной машины

Рассмотрим далее изменения, которые происходят с потокосцеплениями обмоток машин при записи их в осях d, q. Для этого в уравнения (1.16) подставим (1.4). Затем в полученные уравнения и (1.4) подставим выражения для индуктивностей (1.9-1.11) и токов (1.12). После относительно большого количества алгебраических и тригонометрических преобразований можно получить следующие выражения: