Дифференциальные уравнения (1.3) напряжений синхронной машины с переменными коэффициентами, учитывающие вращение электрических цепей ротора, могут быть преобразованы в уравнения с постоянными коэффициентами, известные как уравнения Парка - Горева. На основе этих уравнений могут быть разработаны математические модели синхронных двигателей и генераторов.
Смысл выполняемых преобразований, называемых обычно в теории
переходных процессов преобразованиями Парка - Горева, состоит в том, что при
изучении электрических процессов в контурах фаз статора совершается переход от
неподвижной трехосной системы отсчета (А, В, С) к вращающейся вместе с ротором
декартовой системе (d, q).При
этом переменные в исходных уравнениях заменяются новыми переменными, линейно
связанными с исходными. Так, например, действительные токи ![]() можно заменить новыми
фиктивными токами
можно заменить новыми
фиктивными токами ![]() представляющими собой
проекции обобщенного вектора тока на оси d и q и связанными с исходными
токами зависимостями:
представляющими собой
проекции обобщенного вектора тока на оси d и q и связанными с исходными
токами зависимостями:
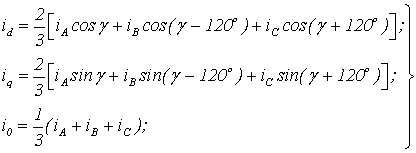 (1.12)
(1.12)
Новые переменные ![]() ,
, ![]() ,
,
![]() принято называть продольным,
поперечным и нулевым током статора. Необходимо заметить, что для симметричных
режимов, а при соединении трехфазных обмоток в звезду с изолированной
нейтралью и для несимметричных режимов i0 = 0. Однако если значение нулевого тока статора и отличается
от нуля, то он все равно не оказывает влияния на движение ротора синхронной
машины, так как он не участвует в создании вращающего поля машины. Поэтому при
исследовании электромеханических переходных процессов обычно нулевую составляющую
тока статора не рассматривают.
принято называть продольным,
поперечным и нулевым током статора. Необходимо заметить, что для симметричных
режимов, а при соединении трехфазных обмоток в звезду с изолированной
нейтралью и для несимметричных режимов i0 = 0. Однако если значение нулевого тока статора и отличается
от нуля, то он все равно не оказывает влияния на движение ротора синхронной
машины, так как он не участвует в создании вращающего поля машины. Поэтому при
исследовании электромеханических переходных процессов обычно нулевую составляющую
тока статора не рассматривают.
Рассмотрим теперь геометрическую интерпретацию выполненных
преобразований (1.12). Для этого дадим изображение мгновенных токов на
векторной диаграмме. Мгновенное значение тока или напряжения в трехфазной
симметричной системе векторов тока или напряжения получается как проекция
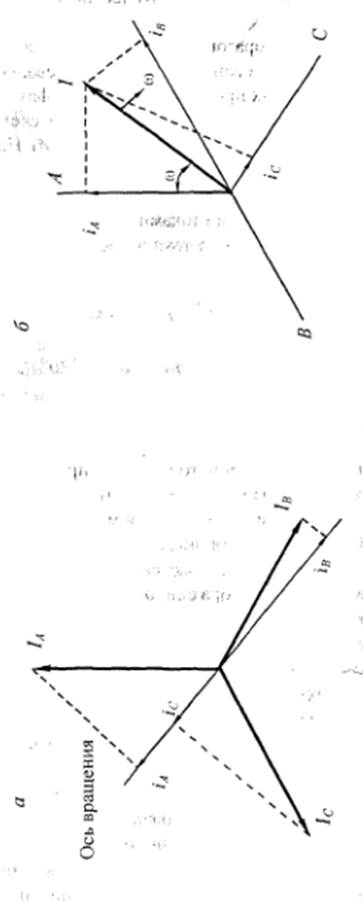
соответствующего вектора на ось времени (рис. 1.4,а).Изменение мгновенных токов во времени можно получить с помощью так
называемого обобщенного или изображающего вектора. Для этого построим вначале
три симметрично расположенные оси времени (А, В,С)
и из центра проведем изображающий вектор ![]() , равный по величине
амплитуде фазных токов (рис. 1.4, б). Если вектор
, равный по величине
амплитуде фазных токов (рис. 1.4, б). Если вектор ![]() вращать
с частотой вращения ротора (
вращать
с частотой вращения ротора (![]() ), то его проекции на оси
дадут значения мгновенных фазных токов
), то его проекции на оси
дадут значения мгновенных фазных токов ![]() . При этом чередование осей
времени (А, В,
С) противоположно чередованию фаз тока, так как оси времени вращаются
навстречу векторам.
. При этом чередование осей
времени (А, В,
С) противоположно чередованию фаз тока, так как оси времени вращаются
навстречу векторам.
Таким образом, с помощью вектора ![]() можно изображать три
симметричных синусоидальных тока, изменяющихся во времени. Действительные фазные
токи, как проекции
можно изображать три
симметричных синусоидальных тока, изменяющихся во времени. Действительные фазные
токи, как проекции ![]() на оси А, В, С (см. рис.
1.4,б)
можно писать в виде
на оси А, В, С (см. рис.
1.4,б)
можно писать в виде
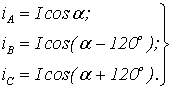 (1.13)
(1.13)
Представим
также токи ![]() и
и ![]() с
помощью изображающего вектора
с
помощью изображающего вектора ![]() на
диаграмме. Для этого построим наряду с тремя осями (А, В, С), поперечную
и продольную оси, вращающиеся вместе с ротором (рис. 1.5). Тогда проекции
изображающего вектора
на
диаграмме. Для этого построим наряду с тремя осями (А, В, С), поперечную
и продольную оси, вращающиеся вместе с ротором (рис. 1.5). Тогда проекции
изображающего вектора ![]() в данном случае дадут
продольный и поперечный токи
в данном случае дадут
продольный и поперечный токи ![]() и
и ![]() , значения
которых на основе рис. 1.5 можно записать в виде
, значения
которых на основе рис. 1.5 можно записать в виде
|
Рис. 1.4. Представление мгновенных фазных тоюв статора: а - с помощью векторов тока; б- с помощью изображающего вектора |
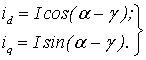 (1.14)
(1.14)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.