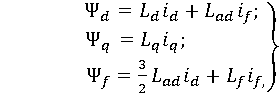Магнитное состояние машины, определяющее синхронное индуктивное сопротивление по продольной оси. Уравнения напряжений синхронной машины. Модель машины с вращающимися щетками при неподвижной обмотке статора

                                                    (1.18)

где   – синхронная продольная индуктивность обмотки статора;

 – синхронная поперечная индуктивность обмотки статора;

 – индуктивность обмотки возбуждения;

 – взаимная индуктивность обмоток статора и ротора в продольной оси.

Характерной особенностью полученных уравнений является отсутствие индуктивностей, зависящих от углового положения ротора, т. е. угла . Поэтому при вычислении производных от потокосцепления по времени операция дифференцирования будет относиться только к токам.

Анализ уравнений (1.18) показывает, что в полученных выражениях потокосцеплений нарушено правило взаимности, согласно которому для магнитносвязанных цепей взаимные индуктивности должны быть одинаковы. В выражении для потокосцепления продольного контура статора  взаимная индуктивность, определяющая потокосцепление от тока обмотки возбуждения, равна , а в выражении для потокосцепления обмотки возбуждения у взаимная индуктивность оси равна 3/2 . Такое различие в выражениях для индуктивностей, определяющих взаимную индукцию полей статора и ротора, объясняется характером принятых преобразований вида (1.12) и (1.16). Более удобно записывать уравнения потокосцеплений в форме, когда принцип взаимности полностью соответствует в отношении индуктивностей магнитносвязанных цепей ротора и статора. Исходные уравнения (1.19) преобразуются к указанной форме, если вместо действительных токов ротора рассматривать уменьшенные в 2/3 раза и вместо действительных индуктивностей цепей ротора - увеличенные в 3/2 раза. Поскольку уравнения синхронной машины обычно записываются в системе относительных единиц, то необходимые преобразования могут быть сделаны одновременно с введением новых параметров, а уравнения (1.18) представлены как:

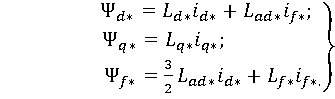                                    (1.19)

В полученных уравнениях для потокосцеплений  и  (индекс относительности величин в дальнейшем для простоты изложения будем опускать) содержатся названные нами поперечная и продольная индуктивности обмотки статора, математически определяемые через коэффициенты собственных и взаимных индуктивностей фазных обмоток машин, согласно выражениям (1.18). Однако индуктивности  и  имеют простой физический смысл. Предположим, что к трехфазной сети с симметричными напряжениями подключена синхронная машина с отключенной системой возбуждения (=0). Если ротор машины вращать с частотой, равной частоте магнитного поля, то ротор и магнитное поле статора будут неподвижны относительно друг друга. Допустим, что в таком синхронном режиме амплитуда магнитного поля совпадает с продольной осью полюсов d. В этом случае будет отсутствовать магнитное поле вдоль оси q, и следовательно, потокосцепление . Таким образом, в рассматриваемом режиме работы машины потокосцепление с обмотками статора будет определяться только величиной Согласно (1.19), равенство может выполняться, только если =0. Поэтому фазные токи статора в данных условиях являются только продольными. Следовательно, индуктивность  из первого уравнения (1.19) при (=0 определится так:

                                                                                    (1.20)

Поскольку для рассматриваемого случая потокосцепление  определяется фазной обмоткой, а ток  равен амплитуде фазного тока, то их отношение (1.20) есть индуктивность фазной обмотки. Однако физически  – это не просто индуктивность какой-либо фазы, а эквивалентная индуктивность, учитывающая взаимные индуктивности с другими фазами. Если  – величина постоянная, то в нашем случае изменение во времени потокосцепления совпадает по фазе с изменением во времени тока. Вследствие этого отношение (1.20) потока к току получается величиной неизменной при вращении ротора.

Таким образом, величина  с физической точки зрения представляет индуктивность фазной обмотки статора при протекании по обмоткам статора симметричных синусоидальных токов прямой последовательности, вращении ротора с синхронной частотой и ориентации поля токов статора по продольной оси. Соответствующее сопротивление  называется синхронным индуктивным сопротивлением по продольной оси. На рис. 1.8 показаны состояние обмоток машины (а) и условная картина магнитного поля (б), соответствующая сопротивлению обмотки статора, равному  Следует отметить, что при принятых условиях магнитный поток относительно ротора неподвижен, и поэтому он и потокосцепление обмотки возбуждения не меняются в зависимости от состояния обмотки, замкнута она или, как показано на рис. 1.8, а, разомкнута. Если при принятом режиме ориентации магнитного поля по оси d (рис. 1.8, б) выполнить замеры фазного напряжения , тока  и мощности  синхронной машины, то можно определить полное, активное и индуктивное сопротивления